
【题目】已知z是复数,z+2i, ![]() 均为实数(i为虚数单位),且复数(z+ai)2在复平面上对应的点在第一象限,求实数a的取值范围.
均为实数(i为虚数单位),且复数(z+ai)2在复平面上对应的点在第一象限,求实数a的取值范围.
【答案】解:设复数z=m+ni(m,n∈R), 由题意得z+2i=m+ni+2i=m+(n+2)i∈R,
∴n+2=0,即n=﹣2.
又∵ ![]() ,
,
∴2n+m=0,即m=﹣2n=4.∴z=4﹣2i.
∵(z+ai)2=(4﹣2i+ai)2=[4+(a﹣2)i]2=16﹣(a﹣2)2+8(a﹣2)i
对应的点在复平面的第一象限,横标和纵标都大于0,
∴ 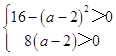
解得a的取值范围为2<a<6
【解析】设出复数的代数形式,整理出代数形式的结果,根据两个都是实数虚部都等于0,得到复数的代数形式.代入复数(z+ai)2 , 利用复数的加减和乘方运算,写出代数的标准形式,根据复数对应的点在第一象限,写出关于实部大于0和虚部大于0,解不等式组,得到结果.


科目:高中数学 来源: 题型:
【题目】已知f(x)=(x2﹣2ax)ebx , x为自变量.
(1)函数f(x)分别在x=﹣1和x=1处取得极小值和极大值,求a,b.
(2)若a≥0且b=1,f(x)在[﹣1,1]上是单调函数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,其中a>0.
,其中a>0.
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间![]() 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z=(a2﹣7a+6)+(a2﹣5a﹣6)i(a∈R)
(1)若复数z为纯虚数,求实数a的值;
(2)若复数z在复平面内的对应点在第四象限,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题.他们在沙滩上画点或用小石子表示数,按照点或小石子能排列的形状对数进行分类.如下图中实心点的个数5,9,14,20,…为梯形数.根据图形的构成,记此数列的第2013项为a2013 , 则a2013﹣5=( ) 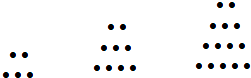
A.2019×2013
B.2019×2012
C.1006×2013
D.2019×1006
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,{bn}是等比数列,且b2=3,b3=9,a1=b1 , a14=b4 . (Ⅰ)求{an}的通项公式;
(Ⅱ)设cn=an+bn , 求数列{cn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法点拨:学生的学习积极性与对待班级工作的态度是否有关系?并说明理由.(参考下表)
P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com