
【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法点拨:学生的学习积极性与对待班级工作的态度是否有关系?并说明理由.(参考下表)
P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:高中数学 来源: 题型:
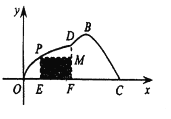
【题目】如图所示,某小区为美化环境,准备在小区内草坪的一侧修建一条直路![]() ,另一侧修建一条休闲大道,它的前一段
,另一侧修建一条休闲大道,它的前一段![]() 是函数
是函数![]() ,
, ![]() 的一部分,后一段
的一部分,后一段![]() 是函数
是函数![]() (
(![]() ,
, ![]() ),
),![]() 时的图象,图象的最高点为
时的图象,图象的最高点为![]() ,
, ![]() ,垂足为
,垂足为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若在草坪内修建如图所示的儿童游乐园PMFE,问点![]() 落在曲线
落在曲线![]() 上何处时,儿童乐园的面积最大?
上何处时,儿童乐园的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
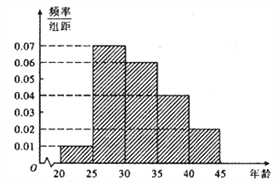 (2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
(2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,若不等式f(﹣2m2+2m﹣1)+f(8m+ek)>0(e是自然对数的底数),对任意的m∈[﹣2,4]恒成立,则整数k的最小值是( )
,若不等式f(﹣2m2+2m﹣1)+f(8m+ek)>0(e是自然对数的底数),对任意的m∈[﹣2,4]恒成立,则整数k的最小值是( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某企业有甲、乙两个研发小组.为了比较他们的研发水平,现随机抽取这两个小组往年研发新产品的结果如下:(a,b),(a,![]() ),(a,b),(
),(a,b),(![]() ,b),(
,b),(![]() ,
,![]() ),(a,b),(a,b),(a,
),(a,b),(a,b),(a,![]() ),(
),(![]() ,b),(a,
,b),(a,![]() ),(
),(![]() ,
,![]() ),(a,b),(a,
),(a,b),(a,![]() ),(
),(![]() ,b),(a,b).其中a,
,b),(a,b).其中a,![]() 分别表示甲组研发成功和失败;b,
分别表示甲组研发成功和失败;b,![]() 分别表示乙组研发成功和失败.
分别表示乙组研发成功和失败.
(I)若某组成功研发一种新产品,则给该组记1分,否则记0分.试计算甲、乙两组研发新产品的成绩的平均数和方差,并比较甲、乙两组的研发水平;
(II)若该企业安排甲、乙两组各自研发一种新产品,试估计恰有一组研发成功的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校5个学生的数学和物理成绩如表
学生的编号i | 1 | 2 | 3 | 4 | 5 |
数学xi | 80 | 75 | 70 | 65 | 60 |
物理yi | 70 | 66 | 68 | 64 | 62 |
(Ⅰ)假设在对这5名学生成绩进行统计时,把这5名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有2名学生的物理成绩是自己的实际分数的概率是多少?
(Ⅱ)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系的,在上述表格是正确的前提下,用x表示数学成绩,用y表示物理成绩,求y与x的回归方程;
参考公式: ![]() =
= 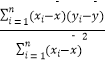 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3﹣2ax2+3a2x+b(a>0).
x3﹣2ax2+3a2x+b(a>0).
(1)当y=f(x)的极小值为1时,求b的值;
(2)若f(x)在区间[1,2]上是减函数,求a的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com