练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    计算：÷0.06250.25；


    解　(1)原式＝


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在“綈p”，“p∧q”，“p∨q”形式的命题中“p∨q”为真，“p∧q”为假，“綈p”

    为真，那么p，q的真假为p______，q______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设abc>0，二次函数f(x)＝ax2＋bx＋c的图象可能是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)＝loga (a>0，a≠1)．

    (1)求f(x)的定义域；

    (2)判断f(x)的奇偶性并予以证明；

    (3)求使f(x)>0的x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝|2x－1|，a<b<c，且f(a)>f(c)>f(b)，则下列结论中，一定成立的是________．

    ①a<0，b<0，c<0;  ②a<0，b≥0，c>0；③2－a<2c;  ④2a＋2c<2.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设偶函数f(x)满足f(x)＝2x－4(x≥0)，则{x|f(x－2)>0}＝____________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    定义在R上的偶函数f(x)满足f(x＋1)＝－f(x)，且在[－1，0]上是增函数，给出下列关于

    f(x)的判断：

    ①f(x)是周期函数；

    ②f(x)关于直线x＝1对称；

    ③f(x)在[0,1]上是增函数；

    ④f(x)在[1,2]上是减函数；

    ⑤f(2)＝f(0)．

    其中正确的序号是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝lg(x－1)的定义域是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


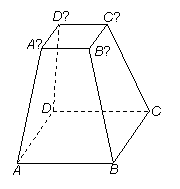
    先阅读：如图，设梯形ABCD的上、下底边的长分别是a，b（a＜b），高为h，求梯形的面积．

     


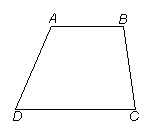    方法一：延长DA、CB交于点O，过点O作CD的垂线分别交AB、CD于E，F，则．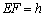

    设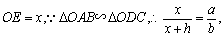即．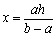

                ．

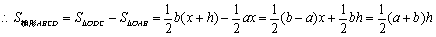    方法二：作AB的平行线MN分别交AD、BC于M、N，过点A作BC的平行线AQ分别交MN、DC于P、Q，则．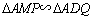

    设梯形AMNB的高为，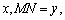

    ．

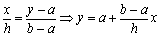        已知四棱台ABCD－A′B′C′D′的上、下底面的面积分别是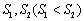，棱台的高为h，类比以上两种方法，分别求出棱台的体积（棱锥的体积=底面积高）．

    查看答案和解析>>

    同步练习册答案