
分析 求出方程x2-3x+4=0的判别式△后即求出A,再求出(x+1)(x2+3x-4)=0的根即求出B,再由条件列出集合B的非空子集即为集合P.
解答 解:由于方程x2-3x+4=0的判别式△=9-16=-7<0,知A=∅,
由(x+1)(x2+3x-4)=0得,x+1=0或x2+3x-4=0,解得x=-1或1或-4,则B={-1,1,-4},
∵A?P⊆B,∴集合P≠∅,且其元素全属于B,即集合P为集合B的非空子集:
{1}或{-1}或{-4}或{-1,1}或{-1,-4}或{1,-4}或{-1,1,-4}.
点评 本题考查了集合间的包含关系和列举法求已知集合的子集,解题的关键:必须确定满足条件的集合P的元素,即明确A、B,充分把握子集、真子集的概念,准确化简集合是解决问题的首要条件.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
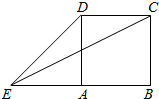 如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED,则sin∠CED-cos∠CED=( )
如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED,则sin∠CED-cos∠CED=( )| A. | -$\frac{\sqrt{10}}{5}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{3\sqrt{10}}{10}$ | D. | $\frac{2\sqrt{10}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
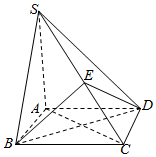 如图,四棱锥S-ABCD的底面是正方形,SA⊥底面ABCD,E是SC上一点.
如图,四棱锥S-ABCD的底面是正方形,SA⊥底面ABCD,E是SC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com