
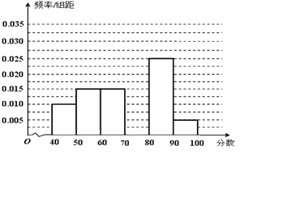
【题目】某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60), ...,[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 从成绩在[40,50)和[90,100]的学生中任选两人,求他们在同一分数段的概率.
【答案】(Ⅰ)成绩落在[70,80)上的频率是0.3,频率分布直方图见解析;
(Ⅱ)及格率(60分及以上为及格)为: 75﹪,平均分: 71;(Ⅲ) ![]() .
.
【解析】试题分析;(Ⅰ)根据频率分布直方图,用1减去成绩落在其它区间上的频率,即得成绩落在![]() 上的频率,从而补全频率分步直方图.
上的频率,从而补全频率分步直方图.
(Ⅱ) 先根据频率分布直方图,用1减去成绩落在![]() 上的频率,即可得到这次考试的及格率.
上的频率,即可得到这次考试的及格率.
(Ⅲ) 成绩在![]() 的学生人数为
的学生人数为![]() 人,在
人,在![]() 的学生人数为3人
的学生人数为3人
用![]() 表示“从成绩在
表示“从成绩在![]() 和
和![]() 的学生中任选两人,他们的成绩在同一分数段”,
的学生中任选两人,他们的成绩在同一分数段”, ![]() 表示“所选两人成绩落在
表示“所选两人成绩落在![]() 内”,
内”, ![]() 表示“所选两人成绩落在
表示“所选两人成绩落在![]() 内”,则
内”,则![]() 和
和![]() 是互斥事件,由互斥事件的概率可得他们在同一分数段的概率.
是互斥事件,由互斥事件的概率可得他们在同一分数段的概率.
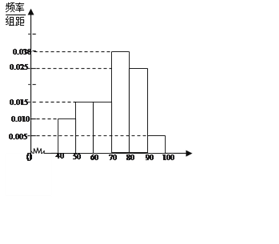
试题解析:(Ⅰ)成绩落在[70,80)上的频率是0.3,频率分布直方图如下图.
 (Ⅱ) 估计这次考试的及格率(60分及以上为及格)
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)
为:1![]() 0.01×10
0.01×10![]() 0.015×10=75﹪
0.015×10=75﹪
平均分:45×0.1+55×0.15+65×0.15+75×0.3
+85×0.25+95×0.05=71
(Ⅲ) 成绩在[40,50)的学生人数为
0.010×10×60=6
在[90,100)的学生人数为
0.005×10×60=3
用A表示“从成绩在[40,50)和[90,100]的学生中任选两人,他们的成绩在同一分数段”, ![]() 表示“所选两人成绩落在[40,50)内”,
表示“所选两人成绩落在[40,50)内”, ![]() 表示“所选两人成绩落在[90,100]内”,则
表示“所选两人成绩落在[90,100]内”,则![]() 和
和![]() 是互斥事件,且
是互斥事件,且
![]() , 从而
, 从而![]() ,
,
因为![]() 中的基本事件个数为15,
中的基本事件个数为15, ![]() 中的基本事件个数为3,全部基本事件总数为36,
中的基本事件个数为3,全部基本事件总数为36,
所以 所求的概率为![]() .
.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】某工厂修建一个长方体无盖蓄水池,其容积为6400立方米,深度为4米.池底每平方米的造价为120元,池壁每平方米的造价为100元.设池底长方形的长为x米.
(Ⅰ)求底面积,并用含x的表达式表示池壁面积;
(Ⅱ)怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
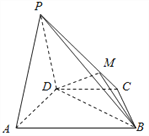
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直角梯形ABCD中,AD∥BC,∠ADC=90°,A(-3,-10),
B (-2,-1),C(3,4),
(1)求边AD和CD所在的直线方程;
(2)数列![]() 的前
的前![]() 项和为
项和为![]() ,点
,点![]() 在直线CD上,求证
在直线CD上,求证![]() 为等比数列.
为等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,对于函数
为坐标原点,对于函数![]() ,称向量
,称向量![]() 为函数
为函数![]() 的伴随向量,同时称函数
的伴随向量,同时称函数![]() 为向量
为向量![]() 的伴随函数.
的伴随函数.
(Ⅰ)设函数![]() ,试求
,试求![]() 的伴随向量
的伴随向量![]() ;
;
(Ⅱ)记向量![]() 的伴随函数为
的伴随函数为![]() ,求当
,求当![]() 且
且![]() 时
时![]() 的值;
的值;
(Ⅲ)由(Ⅰ)中函数![]() 的图像(纵坐标不变)横坐标伸长为原来的
的图像(纵坐标不变)横坐标伸长为原来的![]() 倍,再把整个图像向右平移
倍,再把整个图像向右平移![]() 个单位长度得到
个单位长度得到![]() 的图像。已知
的图像。已知![]()
![]() ,问在
,问在![]() 的图像上是否存在一点
的图像上是否存在一点![]() ,使得
,使得![]() .若存在,求出
.若存在,求出![]() 点坐标;若不存在,说明理由。
点坐标;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 的离心率为
的离心率为![]() ,过左焦点作x轴的垂线交椭圆于A、B两点,且|AB|=1.
,过左焦点作x轴的垂线交椭圆于A、B两点,且|AB|=1.
(1)求椭圆E的方程;
(2)设P、Q是椭圆E上两点,P在第一象限,Q在第二象限,且OP⊥OQ,其中O是坐标原点.
当P、Q运动时,是否存在定圆O,使得直线PQ都与定圆O相切?若存在,请求出圆O的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 和抛物线
和抛物线![]() 交于
交于![]() ,
,![]() 两点,且直线
两点,且直线![]() 恰好通过椭圆
恰好通过椭圆![]() 的右焦点.
的右焦点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)经过椭圆![]() 右焦点的直线
右焦点的直线![]() 和椭圆
和椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 在椭圆上,且
在椭圆上,且![]() ,其中
,其中![]() 为坐标原点,求直线
为坐标原点,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com