【答案】
分析:根据题意,由一元二次方程的性质,可得x
2+2ax+b=0有实根的充要条件为b≤a
2,
(1)由题意分析可得,这是几何概型,将
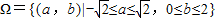
表示为平面区域,进而可得其中满足b≤a
2的区域的面积,由几何概型公式,计算可得答案.
(2)由题意分析可得,这是古典概型,由a、b分别从{-1,0,1},{0,1,2}中任取的数字,易得一共可以得到9个不同方程;可得满足b≤a
2的全部情况数目,结合古典概型公式,计算可得答案.
解答:解:方程x
2+2ax+b=0有实根?△≥0?4a
2-4b≥0?b≤a
2,
(1)点(a,b)所构成的区域为
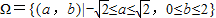
,
面积S
Ω=
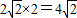
;
设“方程有实根”为事件A,所对应的区域为
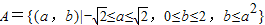
,
其面积
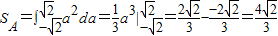
,
这是一个几何概型,所以
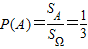
(2)因为a∈Z,b∈Z,所以(a,b)的所有可能取值有9个,分别是:(-1,0),(0,0),(1,0),(-1,1),(0,1),(1,1),(-1,2),(0,2),(1,2),
其中,满足△≥0即b≤a
2的有5个:(-1,0),(0,0),(1,0),(-1,1),(1,1).
设“方程有实根”为事件B,这是一个古典概型,所以
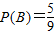
答:(1)所求概率为

;(2)所求概率为

.
点评:本题考查几何概型和古典概型,放在一起的目的是把两种概型加以比较,注意两者的不同.

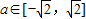 ,b∈[0,2].
,b∈[0,2].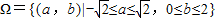 表示为平面区域,进而可得其中满足b≤a2的区域的面积,由几何概型公式,计算可得答案.
表示为平面区域,进而可得其中满足b≤a2的区域的面积,由几何概型公式,计算可得答案.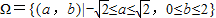 ,
,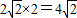 ;
;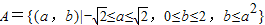 ,
,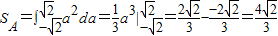 ,
,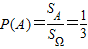
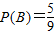
 ;(2)所求概率为
;(2)所求概率为 .
.
