
已知函数f(x)=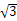 sin ωx+cos ωx+c(ω>0,x∈R,c是实数常数)的图象上的一个最高点是(
sin ωx+cos ωx+c(ω>0,x∈R,c是实数常数)的图象上的一个最高点是( ,1),与该最高点最近的一个最低点是(
,1),与该最高点最近的一个最低点是(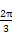 ,-3),
,-3),
(1)求函数f(x)的解析式及其单调增区间;
(2)在△ABC中,角A、B、C所对的边分别为a,b,c,且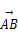 ·
·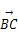 =-
=- ac,角A的取值范围是区间M,当x∈M时,试求函数f(x)的取值范围.
ac,角A的取值范围是区间M,当x∈M时,试求函数f(x)的取值范围.
解:(1)∵f(x)=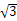 sin ωx+cos ωx+c,
sin ωx+cos ωx+c,
∴f(x)=2sin(ωx+ )+c,
)+c,
∵( ,1)和(
,1)和(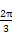 ,-3)分别是函数图象上相邻的最高点和最低点,
,-3)分别是函数图象上相邻的最高点和最低点,
∴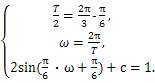 解得
解得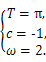
∴f(x)=2sin(2x+ )-1.
)-1.
由2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈Z,解得kπ-
,k∈Z,解得kπ- ≤x≤kπ+
≤x≤kπ+ ,k∈Z.
,k∈Z.
∴函数f(x)的单调递增区间是[kπ- ,kπ+
,kπ+ ],k∈Z.
],k∈Z.
(2)∵在△ABC中,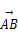 ·
·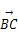 =-
=- ac,
ac,
∴accos(π-B)=- ac,0<B<π,B=
ac,0<B<π,B= .
.
∴A+C=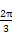 ,0<C,即0<A<
,0<C,即0<A<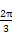 .
.
∴M=(0,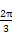 ).
).
当x∈M时, <2x+
<2x+ <
<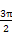 ,考察正弦函数y=sinx的图象,可知,-1<sin(2x+
,考察正弦函数y=sinx的图象,可知,-1<sin(2x+ )≤1.
)≤1.
∴-3<f(x)≤1,即函数f(x)的取值范围是(-3,1].


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
已知函数f(x)=Asin ωx(A>0,ω>0)的最小正周期为2,且f( )=1,则函数y=f(x)的图象向左平移
)=1,则函数y=f(x)的图象向左平移 个单位所得图象的解析式为( )
个单位所得图象的解析式为( )
(A)y=2sin(πx+ )
)
(B)y= sin(πx-
sin(πx- )
)
(C)y=2sin(πx+ )
)
(D)y= sin(πx+
sin(πx+ )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=sin x+sin(x+ ).
).
(1)求f(x)的最小值,并求使f(x)取得最小值的x的集合;
(2)不画图,说明函数y=f(x)的图象可由y=sin x的图象经过怎样的变化得到.
查看答案和解析>>
科目:高中数学 来源: 题型:
.已知向量a=(2cos x,1),b=(cos x, sin 2x),函数f(x)=a·b.
sin 2x),函数f(x)=a·b.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)当x∈[ ,
, ]时,若f(x)=
]时,若f(x)= ,求f(x-
,求f(x- )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
)设△ABC的三个内角A,B,C成等差数列,且(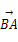 +
+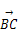 )·
)·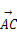 =0,则△ABC的形状是( )
=0,则△ABC的形状是( )
(A)直角三角形 (B)钝角三角形
(C)等边三角形 (D)等腰非等边三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com