
| A. | $\frac{1}{16}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
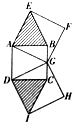 折纸已经成为开发少年儿童智力的一大重要工具和手段.已知在折叠“爱心”的过程中会产生如图所示的几何图形,其中四边形ABCD为正方形,G为线段BC的中点,四边形AEFG与四边形DGHI也为正方形,连接EB,CI,则向多边形AEFGHID中投掷一点,该点落在阴影部分内的概率为$\frac{\sqrt{3}}{5}$.
折纸已经成为开发少年儿童智力的一大重要工具和手段.已知在折叠“爱心”的过程中会产生如图所示的几何图形,其中四边形ABCD为正方形,G为线段BC的中点,四边形AEFG与四边形DGHI也为正方形,连接EB,CI,则向多边形AEFGHID中投掷一点,该点落在阴影部分内的概率为$\frac{\sqrt{3}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
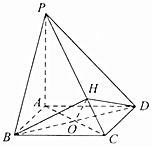 如图,四棱锥P-ABCD的底面是边长为2的正方形,PA⊥平面ABCD,AC交BD于O,H为线段PC上一点.
如图,四棱锥P-ABCD的底面是边长为2的正方形,PA⊥平面ABCD,AC交BD于O,H为线段PC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | -1 | C. | -$\frac{1}{2}$ | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com