
分析 (Ⅰ)设M(x,y),则$\frac{y+1}{x}•\frac{y-1}{x}$=-$\frac{1}{2}$,化简即可求动点M的轨迹E的方程;
(Ⅱ)直线y=x+m代入椭圆方程,求出|AB|,|MP|,可得△PAB的面积,配方,即可求出三角形面积的最大值.
解答 解:(Ⅰ)设M(x,y),则$\frac{y+1}{x}•\frac{y-1}{x}$=-$\frac{1}{2}$,化简为$\frac{{x}^{2}}{2}+{y}^{2}$=1(x≠0);
(Ⅱ)y=x+m代入椭圆方程,消去y得3x2+4mx+2m2-2=0
∵直线l与椭圆有两个交点,
∴△>0,可得m2<3(*)--
设A(x1,y1),B(x2,y2),
∴x1+x2=-$\frac{4m}{3}$,x1x2=$\frac{2{m}^{2}-2}{3}$,
∴弦长|AB|=$\sqrt{2}$|x1-x2|=$\frac{2\sqrt{2}}{3}•\sqrt{6-2{m}^{2}}$,
AB中点M(-$\frac{2m}{3}$,$\frac{m}{3}$),设P(x,0),∴kAB•kMP=-1,
∴$\frac{\frac{m}{3}}{-\frac{2m}{3}-x}$•1=-1,
∴x=-$\frac{m}{3}$,
∴P(-$\frac{m}{3}$,0),|PM|=$\frac{\sqrt{2}|m|}{3}$,
∴S=$\frac{1}{2}$|AB||MP|=$\frac{2}{9}\sqrt{-2({m}^{2}-\frac{3}{2})^{2}+\frac{9}{2}}$
∵m2<3,∴m2=$\frac{3}{2}$时,Smax=$\frac{\sqrt{2}}{3}$.
点评 待定系数法是解决椭圆标准方程的关键,直线与圆锥曲线联立,是解决弦长问题的常用方法.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:解答题
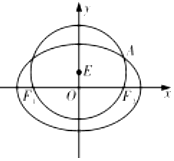 如图,已知圆E:x2+(y-1)2=4经过椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.
如图,已知圆E:x2+(y-1)2=4经过椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
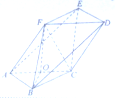 如图,在以A,B,C,D,E,F为顶点的多面体中,四边形ACDF是菱形,∠FAC=60°,AB∥DE,BC∥EF,AB=BC=3,AF=2$\sqrt{3},BF=\sqrt{15}$.
如图,在以A,B,C,D,E,F为顶点的多面体中,四边形ACDF是菱形,∠FAC=60°,AB∥DE,BC∥EF,AB=BC=3,AF=2$\sqrt{3},BF=\sqrt{15}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{16}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com