
【题目】已知数列{an}(n∈N*)是首项为20的等差数列,其公差d≠0,且a1 , a4 , a5成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{an}的前n项和为Sn , 当Sn>0时,求n的最大值;
(Ⅲ)设bn=5﹣ ![]() ,求数列{
,求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
【答案】解:(Ⅰ)数列{an}(n∈N*)是首项为20的等差数列,其公差d≠0,
且a1,a4,a5成等比数列,
可得a42=a1a5,
即为(20+3d)2=20(20+4d),
解得d=﹣ ![]() (d=0舍去),
(d=0舍去),
数列{an}的通项公式为an=20﹣ ![]() (n﹣1)=
(n﹣1)= ![]() ;
;
(Ⅱ)设数列{an}的前n项和为Sn,
可得Sn=20n﹣ ![]() n(n﹣1)
n(n﹣1) ![]() =﹣
=﹣ ![]() (n2﹣10n)>0,
(n2﹣10n)>0,
解得0<n<10,
则n的最大值为9;
(Ⅲ)bn=5﹣ ![]() =5﹣
=5﹣ ![]() =﹣
=﹣ ![]() (1﹣n),
(1﹣n),
数列 ![]() =
= ![]()
![]()
= ![]() (
( ![]() ﹣
﹣ ![]() ),
),
可得前n项和Tn= ![]() (1﹣
(1﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() )
)
= ![]() ×(1﹣
×(1﹣ ![]() )=
)= ![]() .
.
【解析(1)根据数列{an}是等差数列,表示出a1,a4,a5,再根据它们成等比数列,代入等式a42=a1a5,即可得出公差d,从而可得其通项公式,(2)根据等差数列的求和公式表示出Sn,由Sn>0,解出0<n<10,n为正整数,可得n的最大值为9,(3)由(1)的通项公式表示出bn,通过裂项相消求出其前n想和Tn.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系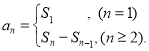 ),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.
),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)设二面角D﹣AE﹣C为60°,AP=1,AD= ![]() ,求三棱锥E﹣ACD的体积.
,求三棱锥E﹣ACD的体积.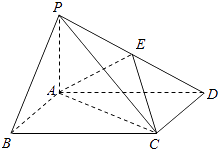
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知sin(A+C)=8sin2 ![]() .
.
(1)求cosB;
(2)若a+c=6,△ABC的面积为2,求b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校对高一年级学生的数学成绩进行统计,全年级同学的成绩全部介于60分与100分之间,将他们的成绩数据绘制如图所示的频率分布直方图.现从全体学生中,采用分层抽样的方法抽取80名同学的试卷进行分析,则从成绩在[80,100]内的学生中抽取的人数为( )
A.56
B.32
C.24
D.18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两位同学进行乒乓球比赛,甲获胜的概率为0.4,现采用随机模拟的方法估计这两位同学打3局比赛甲恰好获胜2局的概率:先利用计算器产生0到9之间取整数值的随机数,制定1,2,3,4表示甲获胜,用5,6,7,8,9,0表示乙获胜,再以每三个随机数为一组,代表3局比赛的结果,经随机模拟产生了30组随机数
102 231 146 027 590 763 245 207 310 386 350 481 337 286 139
579 684 487 370 175 772 235 246 487 569 047 008 341 287 114
据此估计,这两位同学打3局比赛甲恰好获胜2局的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知0<a<1,函数f(x)=logax.
(1)若f(5a﹣1)≥f(2a),求实数a的最大值;
(2)当a= ![]() 时,设g(x)=f(x)﹣3x+2m,若函数g(x)在(1,2)上有零点,求实数m的取值范围.
时,设g(x)=f(x)﹣3x+2m,若函数g(x)在(1,2)上有零点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆M: ![]() +
+ ![]() =1(a>0)的一个焦点为F(﹣1,0),左右顶点分别为A,B,经过点F的直线l与椭圆M交于C,D两点.
=1(a>0)的一个焦点为F(﹣1,0),左右顶点分别为A,B,经过点F的直线l与椭圆M交于C,D两点.
(Ⅰ)求椭圆方程;
(Ⅱ)记△ABD与△ABC的面积分别为S1和S2 , 求|S1﹣S2|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com