有六节电池,其中有2节没电,4节有电,每次随机抽取一个测试,不放回,直至分清楚有电没电为止,
(Ⅰ)求“第二次测出的电池没电的情况下第三次测出的电池也没电”的概率.
(Ⅱ)所要测试的次数ξ为随机变量,求ξ的分布列和数学期望Eξ.
【答案】
分析:(Ⅰ)法一:设事件A=“第二次测出的电池没电”,B=“第三次测出的电池也没电”,由题设条件知
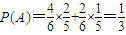
,
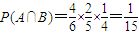
,再由条件概率公式能求出“第二次测出的电池没电的情况下第三次测出的电池也没电”的概率.
法二:设A=“第二次测出的电池没电的情况下第三次测出的电池也没电”,结合题设条件利用古典概型能够求出“第二次测出的电池没电的情况下第三次测出的电池也没电”的概率.
(Ⅱ)ξ的可能取值为2,3,4,5,
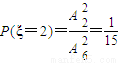
,
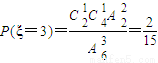
,
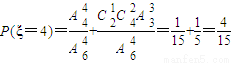
,
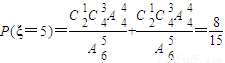
,由此能求出ξ的分布列和Eξ.
解答:解:(Ⅰ)解法一:
设事件A=“第二次测出的电池没电”,
B=“第三次测出的电池也没电”,
则
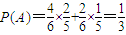
,
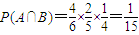
,(2分)
所以
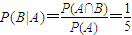
.(4分)
解法二:设A=“第二次测出的电池没电的情况下第三次测出的电池也没电”,
则
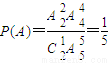
(4分)
(Ⅱ)ξ的可能取值为2,3,4,5,
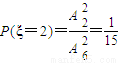
,
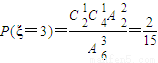
,
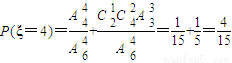
,
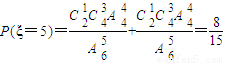
,(8分)
∴分布列为
(10分)
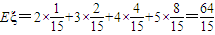
.(12分)
点评:本题考查古典概型和条件概率的求法,考查离散型随机就是的期望和方差.理解古典概型的特征:试验结果的有限性和每一个试验结果出现的等可能性,体现了化归的重要思想,掌握列举法,学会运用分类讨论的思想解决概率的计算问题.易错点是审题不全面,导致出错.

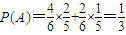 ,
,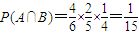 ,再由条件概率公式能求出“第二次测出的电池没电的情况下第三次测出的电池也没电”的概率.
,再由条件概率公式能求出“第二次测出的电池没电的情况下第三次测出的电池也没电”的概率.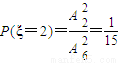 ,
,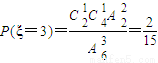 ,
,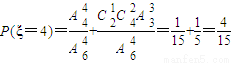 ,
,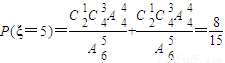 ,由此能求出ξ的分布列和Eξ.
,由此能求出ξ的分布列和Eξ.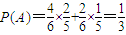 ,
,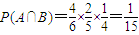 ,(2分)
,(2分)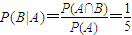 .(4分)
.(4分)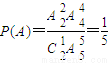 (4分)
(4分)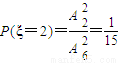 ,
,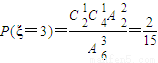 ,
,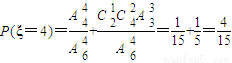 ,
,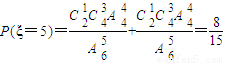 ,(8分)
,(8分)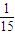
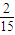
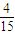
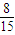
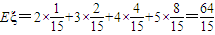 .(12分)
.(12分)
