练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    过点A（-1，-2）且与椭圆
    x2
    6
    +
    y2
    9
    =1有相同焦点的双曲线的标准方程是
     
    ．
    考点：双曲线的标准方程,椭圆的简单性质
    专题：圆锥曲线的定义、性质与方程
    分析：由已知设双曲线方程为
    y2
    a2
    -
    x2
    3-a2
    =1    ，把A（-1，-2）代入，能求出双曲线的标准方程．
    解答： 解：∵椭圆
    x2
    6
    +
    y2
    9
    =1的焦点为F1（0，-
    		3
    ），F2（0，
    		3
    ），
    ∴所求双曲线的焦点为F1（0，-
    		3
    ），F2（0，
    		3
    ），
    设双曲线方程为
    y2
    a2
    -
    x2
    3-a2
    =1    ，
    把A（-1，-2）代入，得：
    4
    a2
    -
    1
    3-a2
    =1，
    解得a2=2或a2=6（舍），
    ∴双曲线的标准方程为
    y2
    2
    -x2=1    ．
    故答案为：
    y2
    2
    -x2=1    ．
    点评：本题考查双曲线标准方程的求法，是基础题，解题时要认真审题，注意双曲线和椭圆性质的合理运用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知椭圆C的离心率为
    		2
    2
    ，椭圆C的右焦点F2和抛物线y2=4
    		2
    x的焦点重合，椭圆C与y轴的一个交点为N，且M是椭圆C的右顶点．
    （1）求tan∠NF2M的值；
    （2）当过点P（4，1）的动直线l与椭圆C相交于两不同点A，B时，在线段AB上取点Q，满足|
    AP
    |•|
    QB
    |-|
    PB
    |•|
    AQ
    |=
    		1-t2
    +
    		t2-1
    （t∈R），求点Q的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

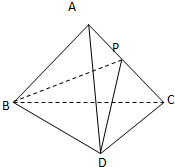    已知△ABC和△DBC是两个有公共斜边的直角三角形，并且AB=AD=AC=2a，CD=
    		6
    a．
    （1）若P是AC边上的一点，当△PBD的面积最小时，求二面角P-BD-A的平面角的正切值；
    （2）能否找到一个球，使A，B，C，D都在该球面上，若不能，请说明理由；若能，求该球的内接圆柱的表面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，a=2，A=45°，若此三角形有两解，则b的范围为（　　）
    A、2＜b＜2
    		2
    B、b＞2
    C、b＜2
    D、
    1
    2
    ＜b＜
    		2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    点A（-1，2，1）在x轴上的投影点和在xOy平面上的投影点的坐标分别为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数y=f（x）是定义在R上的奇函数，且当x∈[0，+∞）时是增函数，则不等式f(2x+
    1
    2
    )＜0    的解集为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，内角A，B，C对边的边长分别是a，b，c，已知c=2．
    （Ⅰ）若C=
    π
    3
    ，且△ABC的面积等于
    		3
    ，求a，b；
    （Ⅱ）若sinC+sin（B-A）=2sin2A，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若f（lgx）=x，则f（3）=（　　）
    A、103
    B、3
    C、lg3
    D、310

    查看答案和解析>>

    科目：高中数学 来源： 题型：

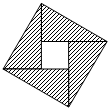    三国时期赵爽在《勾股方圆图注》中对勾股定理的证明可用现代数学表述为如图所示，我们教材中利用该图作为“（　　）”的几何解释．
    A、如果a＞b，b＞c，那么a＞c
    B、如果a＞b＞0，那么a2＞b2
    C、对任意实数a和b，有a2+b2≥2ab，当且仅当a=b时等号成立
    D、如果a＞b，c＞0那么ac＞bc

    查看答案和解析>>

    同步练习册答案