练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中，∠ACB＝90°，AB＝8，∠ABC＝60°，PC⊥平面ABC，PC＝4，M是AB上一个动点，则PM的最小值为__________．



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    若函数在区间内是增函数，则实数的取值范围是    （　　）

    A.          B.           C .            D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若椭圆的两焦点为（－2，0）和（2，0），且椭圆过点，则椭圆方程是（    ）

           A．            B．            C．   D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列命题正确的是（    ）

    A、若两条直线和同一个平面所成的角相等，则这两条直线平行

    B、若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行

    C、若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行

    D、若两个平面都垂直于第三个平面，则这两个平面平行

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     将一个真命题中的“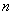个平面”换成“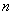条直线”、“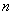条直线”换成“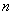个平面”，若所得到的新命题仍是真命题，则该命题称为“可换命题”，下列四个命题

       ①垂直于同一个平面的两条直线平行  ②垂直于同一个平面的两个平面平行；

    ③平行于同一条直线的两条直线平行  ④平行于同一个平面的两条直线平行。

    其中是“可换命题”的是（    ）

    A．①②       B．①④       C．①③       D．③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示，已知长方体ABCD—A1B1C1D1中，AB=BC=2，AA1=4，E是棱CC1上的点，且BE⊥B1C.（1）求CE的长；（2）求证：A1C⊥平面BED；（3）求A1B与平面BDE夹角的正弦值.

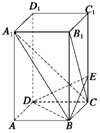
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，将一个四棱锥的每一个顶点染一种颜色，并使同一条棱上的两端点异色，如果只有4种颜色可供使用，则不同的染色方法有……………………(     )

    A．58种              B.60种           C.72种          D.84种

     


    查看答案和解析>>

    科目：高中数学 来源： 题型：


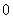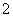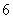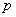
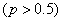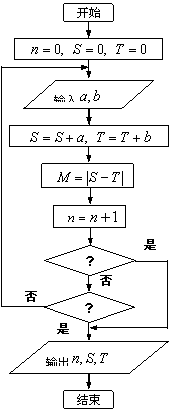
    甲乙两人进行围棋比赛，约定每局胜者得1分，负者得分（不计和棋），比赛进行到有一人比对方多分或打满局时停止．设甲在每局中获胜的概率为，且各局胜负相互独立．已知第二局比赛结束时比赛停止的概率为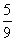．若右图为统计这次比赛的局数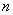和甲、乙的总得分数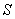、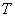的程序框图．其中如果甲获胜则输入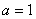， ；如果乙获胜，则输入．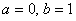

    （1）在右图中，第一、第二两个判断框应分别填

    写什么条件？

    （2）求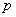的值；

    （3）设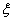表示比赛停止时已比赛的局数，求随机变量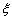的分布列和数学期望． 　　　 

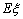    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合，则 (    )

        A．      B．     C．     D．

    查看答案和解析>>

    同步练习册答案