练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列说法正确的是（　　）
    A.某厂一批产品的次品率为 ， 则任意抽取其中10件产品一定会发现一件次品
    B.气象部门预报明天下雨的概率是90%，说明明天该地区90%的地方要下雨，其余10%的地方不会下雨
    C.某医院治疗一种疾病的治愈率为10%，那么前9个病人都没有治愈，第10个人就一定能治愈
    D.掷一枚硬币，连续出现5次正面向上，第六次出现反面向上的概率与正面向上的概率仍然都为0.5

    【答案】D
    【解析】某厂一批产品的次品率为 ，
    则任意抽取其中10件产品一定会发现一件次品说法是错误的，故A不能选
    气象部门预报明天下雨的概率，是说明有多大的把握有雨，而不是具体的什么地方有雨，
    故B不正确，
    某医院治疗一种疾病的治愈率为10%，那么前9个病人都没有治愈，第10个人就一定能治愈
    说法是错误的，治愈率为10%是说明来的所有病人中有10%的被治愈，故C不正确，
    掷一枚硬币，连续出现5次正面向上，第六次出现反面向上的概率与正面向上的概率仍然都为0.5，
    概率是一个固定的值，不随第几次试验有关，故D正确．
    故选D．
    【考点精析】通过灵活运用随机事件，掌握在条件S下可能发生也可能不发生的事件，叫相对于条件S的随机事件即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知等差数列前5项和为50， ，数列的前项和为， ， .

    （Ⅰ）求数列， 的通项公式；

    （Ⅱ）若数列满足, ，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】袋中共有8个球，其中3个红球、2个白球、3个黑球．若从袋中任取3个球，则所取3个球中至多有1个红球的概率是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】【2017江西师范大学附属中学三模】已知函数是自然对数的底数).

    (1)求函数的单调区间;

    (2)若,当时,求函数的最大值;

    (3)若且,求证: .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义max{{x，y}= ，设f（x）=max{ax﹣a，﹣logax}（x∈R+ ， a＞0，a≠1）．若a= ，则f（2）+f（ ）=；若a＞1，则不等式f（x）≥2的解集是

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校研究性学习小组对该校高三学生视力情况进行调查，在高三的全体名学生中随机抽取了名学生的体检表，并得到如图的频率分布直方图．

    年级名次

    是否近视

    近视

    不近视

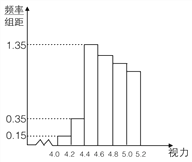
    （1）若直方图中后四组的频数成等差数列，试估计全 年级视力在以下的人数；

    （2）学习小组成员发现，学习成绩突出的学生，近视的比较多，为了研究学生的视力与学习成绩是否有关系，对年级名次在名和名的学生进行了调查，得到右表中数据，根据表中的数据，能否在犯错的概率不超过的前提下认为视力与学习成绩有关系?

    7.879

    附：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （1）当时,求函数在点处的切线方程；

    （2）对任意的函数恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种产品的广告费支出x与销售额y（单位：万元）之间有如下对应数据：

    P（k2＞k）

    0.50

    0.40

    0.25

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    k

    0.455

    0.708

    1.323

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.83

    x

    2

    4

    5

    6

    8

    y

    30

    40

    60

    50

    70

    （Ⅰ）画出散点图；
    （Ⅱ）求回归直线方程；
    （Ⅲ）试预测广告费支出为10万元时，销售额多大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种产品的质量以其质量指标值衡量，并依据质量指标值划分等级如下表：

    质量指标值

    等级

    三等品

    二等品

    一等品

    从某企业生产的这种产品中抽取200件，检测后得到如下的频率分布直方图：

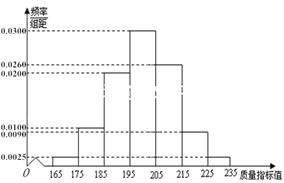
    （Ⅰ）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品92%”的规定？

    （Ⅱ）在样本中，按产品等级用分层抽样的方法抽取8件，再从这8件产品中随机抽取4件，求抽取的4件产品中，一、二、三等品都有的概率；

    （Ⅲ）该企业为提高产品质量，开展了“质量提升月”活动，活动后再抽样检测，产品质量指标值近似满足，则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少？

    查看答案和解析>>

    同步练习册答案