
【题目】已知等差数列![]() 前5项和为50,
前5项和为50, ![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求数列![]() ,
, ![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 满足
满足![]() ,
, ![]() ,求
,求![]() 的值.
的值.
【答案】(1) ![]()
![]() ;(2)
;(2) ![]() .
.
【解析】试题分析: (I)设等差数列{an}的公差为d,利用等差数列的通项公式及其前n项和公式即可首项和公差,即可求出数列{an}的通项公式,再根据数列的递推公式可得所以{bn}为首项为1,公比为4的等比数列,即可求出数列{bn}的通项公式
(II)根据数列的递推公式先求出{cn}的通项公式,再分组求和.
试题解析:
(Ⅰ)设等差数列![]() 的公差为
的公差为![]() .
.
依题意得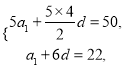 解得
解得![]() ,
, ![]() ,
,
所以![]() .
.
当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
,
![]() ,
,
以上两式相减得![]() ,则
,则![]() ,
,
又![]() ,所以
,所以![]() ,
, ![]() .
.
所以![]() 为首项为1,公比为4的等比数列,
为首项为1,公比为4的等比数列,
所以![]() .
.
(Ⅱ)因为![]() ,
, ![]()
当![]() 时,
时, 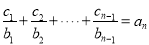 ,
,
以上两式相减得![]() , 所以
, 所以![]() ,
, ![]() .
.
当![]() 时,
时, ![]() ,所以
,所以![]() ,不符合上式,
,不符合上式,
所以![]()
![]()
![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+ ![]() ,曲线f(x)在点(1,f(1))处的切线平行于x轴.
,曲线f(x)在点(1,f(1))处的切线平行于x轴.
(1)求f(x)的最小值;
(2)比较f(x)与 ![]() 的大小;
的大小;
(3)证明:x>0时,xexlnx+ex>x3 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn﹣an}为等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4-4:坐标系与参数方程
已知直线的极坐标方程为![]() ,圆
,圆![]() 的参数方程为
的参数方程为
![]() (其中
(其中![]() 为参数).
为参数).
(Ⅰ)将直线的极坐标方程化为直角坐标方程;
(Ⅱ)求圆![]() 上的点到直线的距离的最小值.
上的点到直线的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 的二项展开式中所有奇数项的系数之和为512,
的二项展开式中所有奇数项的系数之和为512,
(1)求展开式的所有有理项(指数为整数).
(2)求(1﹣x)3+(1﹣x)4+…+(1﹣x)n展开式中x2项的系数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三边长为a,b,c,则下列命题中真命题是( )
A.“a2+b2>c2”是“△ABC为锐角三角形”的充要条件
B.“a2+b2<c2”是“△ABC为钝角三角形”的必要不充分条件
C.“a3+b3=c3”是“△ABC为锐角三角形”的既不充分也不必要条件
D.“ ![]() +
+ ![]() =
= ![]() ”是“△ABC为钝角三角形”的充分不必要条件
”是“△ABC为钝角三角形”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.某厂一批产品的次品率为![]() , 则任意抽取其中10件产品一定会发现一件次品
, 则任意抽取其中10件产品一定会发现一件次品
B.气象部门预报明天下雨的概率是90%,说明明天该地区90%的地方要下雨,其余10%的地方不会下雨
C.某医院治疗一种疾病的治愈率为10%,那么前9个病人都没有治愈,第10个人就一定能治愈
D.掷一枚硬币,连续出现5次正面向上,第六次出现反面向上的概率与正面向上的概率仍然都为0.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com