
【题目】已知函数f(x)=alnx+ ![]() ,曲线f(x)在点(1,f(1))处的切线平行于x轴.
,曲线f(x)在点(1,f(1))处的切线平行于x轴.
(1)求f(x)的最小值;
(2)比较f(x)与 ![]() 的大小;
的大小;
(3)证明:x>0时,xexlnx+ex>x3 .
【答案】
(1)解:f'(x)= ![]() ,根据题意知f'(1)=0,即a=1,∴
,根据题意知f'(1)=0,即a=1,∴ ![]() ,
,
∴f'(x)= ![]() ,∴当0<x<1时,f'(x)<0,f(x)单调递减;
,∴当0<x<1时,f'(x)<0,f(x)单调递减;
当x>1时,f'(x)>0,f(x)单调递增;
∴f(x)min=f(1)=1
(2)解:令 ![]() =
= ![]() =
= ![]() ,
,
![]() ,
,
∴g(x)在(0,+∞)上单调递减
又∵g(1)=0∴当0<x<1时,g(x)>g(1)=0, ![]() ;
;
当x>1时,g(x)<g(1)=0, ![]() ;
;
当x=1时,g(x)=0, ![]()
(3)证明:要证xexlnx+ex>x3,即证: ![]()
令 ![]() ,即证∴f(x)>h(x),
,即证∴f(x)>h(x), ![]() =
= ![]() ,
,
∴当0<x<2时,h'(x)>0,h(x)单调递增;
当x>2时,h'(x)<0,h(x)单调递减;∴h(x)max=h(2)= ![]() ,
,
又由(1)知f(x)min=1,∴f(x)≥1,∴f(x)>h(x),得证
【解析】(1)求出函数的导数,利用曲线f(x)在点(1,f(1))处的切线平行于x轴,求出a,然后判断函数的单调性,求解函数的最小值即可.(2)令 ![]() ,化简通过函数的导数,判断导函数的符号,然后通过x 的范围,判断两个数的大小.(3)要证xexlnx+ex>x3 , 即证:
,化简通过函数的导数,判断导函数的符号,然后通过x 的范围,判断两个数的大小.(3)要证xexlnx+ex>x3 , 即证: ![]() ,令
,令 ![]() ,利用函数的导数,判断函数的单调性求出函数的最小值,即可证明结果.
,利用函数的导数,判断函数的单调性求出函数的最小值,即可证明结果.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,D,E分别是BC,AB的中点,PA⊥平面ABC,∠BAC=90°,AB≠AC,AC>AD,PC与DE所成的角为α,PD与平面ABC所成的角为β,二面角P﹣BC﹣A的平面角为γ,则α,β,γ的大小关系是( ) 
A.α<β<γ
B.α<γ<β
C.β<α<γ
D.γ<β<α
查看答案和解析>>
科目:高中数学 来源: 题型:
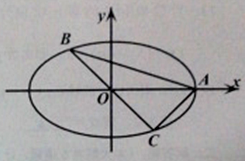
【题目】如图,A,B,C是椭圆M:![]() 上的三点,其中点A是椭圆的右顶点,BC过椭圆M的中心,且满足AC⊥BC,BC=2AC。
上的三点,其中点A是椭圆的右顶点,BC过椭圆M的中心,且满足AC⊥BC,BC=2AC。
(1)求椭圆的离心率;
(2)若y轴被△ABC的外接圆所截得弦长为9,求椭圆方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
已知抛物线![]() 的焦点为
的焦点为![]() ,
, ![]() 为
为![]() 上异于原点的任意一点,过点
上异于原点的任意一点,过点![]() 的直线
的直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,且有
,且有![]() .当点
.当点![]() 的横坐标为
的横坐标为![]() 时,
时, ![]() 为正三角形.
为正三角形.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)若直线![]() ,且
,且![]() 和
和![]() 有且只有一个公共点
有且只有一个公共点![]() ,
,
(ⅰ)证明直线![]() 过定点,并求出定点坐标;
过定点,并求出定点坐标;
(ⅱ)![]() 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学同学的成绩如表:
n | 1 | 2 | 3 | 4 | 5 |
x0 | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6及这6位同学成绩的标准差s;
(2)若从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间[68,75)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若![]() 满足
满足![]() ,且在定义域内
,且在定义域内![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若函数![]() 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数![]() 的最小值;
的最小值;
(Ⅲ)当![]() 时,试比较
时,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市教育部门拟从18名高中数学教师中选拔2人参加省教师技能大赛.为缩短比赛时间,将这18名教师随机分成![]() ,
, ![]() 两组,其选拔赛成绩的茎叶图如图所示.该教育部门先将成绩不低于85分的教师初选出来进行培训后,再从中选拔2人参加省教师技能大赛.
两组,其选拔赛成绩的茎叶图如图所示.该教育部门先将成绩不低于85分的教师初选出来进行培训后,再从中选拔2人参加省教师技能大赛.

(Ⅰ)若仅从初选选手中随机抽选2人参加省赛,并记抽选的2人中来自![]() 组的人数为
组的人数为![]() ,试求
,试求![]() 的分布列和期望值;
的分布列和期望值;
(Ⅱ)在(Ⅰ)的条件下,若参加省赛的2人是同性的概率等于![]() ,求初选出来参加培训的男教师和女教师的人数.
,求初选出来参加培训的男教师和女教师的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(3,﹣4),
=(3,﹣4), ![]() =(6,﹣3),
=(6,﹣3), ![]() =(5﹣x,﹣3﹣y),
=(5﹣x,﹣3﹣y), ![]() =(4,1)
=(4,1)
(1)若四边形ABCD是平行四边形,求x,y的值;
(2)若△ABC为等腰直角三角形,且∠B为直角,求x,y的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com