
【题目】某网站从春节期间参与收发网络红包的手机用户中随机抽取10000名进行调查,将受访用户按年龄分成5组:![]() 并整理得到如下频率分布直方图:
并整理得到如下频率分布直方图:
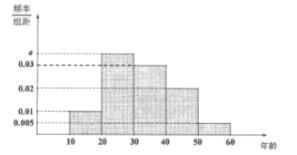
(1)求![]() 的值;
的值;
(2)从春节期间参与收发网络红包的手机用户中随机抽取一人,估计其年龄低于40岁的概率;
(3)估计春节期间参与收发网络红包的手机用户的平均年龄。
 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】某企业用180万元购买一套新设备,该套设备预计平均每年能给企业带来100万元的收入,为了维护设备的正常运行,第一年需要各种维护费用10万元,且从第二年开始,每年比上一年所需的维护费用要增加10万元
(1)求该设备给企业带来的总利润![]() (万元)与使用年数
(万元)与使用年数![]() 的函数关系;
的函数关系;
(2)试计算这套设备使用多少年,可使年平均利润最大?年平均利润最大为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足:|a2﹣a3|=10,a1a2a3=125.
(1)求数列{an}的通项公式;
(2)是否存在正整数m,使得 ![]() ?若存在,求m的最小值;若不存在,说明理由.
?若存在,求m的最小值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔仔细算相还”,其大意为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地”,则该人第五天走的路程为( )
A. 6里B. 12里C. 24里D. 48里
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了了解新生的饮食习惯,在某学院大一年级![]() 名学生中进行了抽样调查,发现喜欢甜品的占
名学生中进行了抽样调查,发现喜欢甜品的占![]() .这
.这![]() 名学生中南方学生共
名学生中南方学生共![]() 人。南方学生中有
人。南方学生中有![]() 人不喜欢甜品.
人不喜欢甜品.
(1)完成下列![]() 列联表:
列联表:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | |||
北方学生 | |||
合计 |
(2)根据表中数据,问是否有![]() 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(3)已知在被调查的南方学生中有![]() 名数学系的学生,其中
名数学系的学生,其中![]() 名不喜欢甜品;有
名不喜欢甜品;有![]() 名物理系的学生,其中
名物理系的学生,其中![]() 名不喜欢甜品.现从这两个系的学生中,各随机抽取
名不喜欢甜品.现从这两个系的学生中,各随机抽取![]() 人,记抽出的
人,记抽出的![]() 人中不喜欢甜品的人数为
人中不喜欢甜品的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:![]() .
.
| 0.15 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com