
已知函数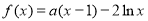 (d为常数)
(d为常数)
(1)当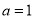 对,求
对,求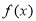 单调区间;
单调区间;
(2)若函数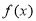 在区间(0,1)上无零点,求a的最大值.
在区间(0,1)上无零点,求a的最大值.
(1)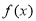 的单调递减区间为
的单调递减区间为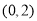 ,单调递增区间为
,单调递增区间为 ;(2)2
;(2)2
【解析】
试题分析:(1)当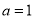 时,先求导函数
时,先求导函数 ,解不等式
,解不等式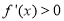 并和定义域求交集得函数
并和定义域求交集得函数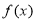 的递增区间,解不等式
的递增区间,解不等式 并和定义域求交集得函数
并和定义域求交集得函数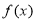 的递减区间;(2)若函数
的递减区间;(2)若函数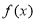 在区间(0,1)上无零点相当于对
在区间(0,1)上无零点相当于对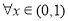 ,
, 恒成立或者
恒成立或者 恒成立,则可转化为求函数
恒成立,则可转化为求函数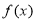 的最值.显然当
的最值.显然当 时,
时, 恒成立,当
恒成立,当 时,先求得
时,先求得 ,令
,令 得,
得,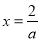 ,分别讨论
,分别讨论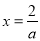 与定义域(0,1)的位置关系,研究函数
与定义域(0,1)的位置关系,研究函数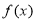 的大致形状,从而求其最值,若最小值大于0则恒正,若最大值小于0则 恒负.
的大致形状,从而求其最值,若最小值大于0则恒正,若最大值小于0则 恒负.
试题解析:(1)当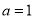 时,函数
时,函数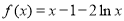 ,
,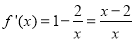
由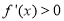 得
得 ,由
,由 得
得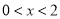
故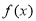 的单调递减区间为
的单调递减区间为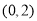 ,单调递增区间为
,单调递增区间为 5分
5分
(2)若函数 在区间
在区间 上无零点,则
上无零点,则
对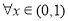 ,
, 恒成立或者
恒成立或者 恒成立.
恒成立.
由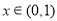 ,得
,得 ,
,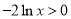 ,
,
故若 ,
,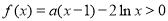 恒成立;
恒成立;
若 ,
, ,
,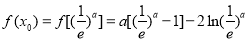

所以,函数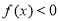 在区间
在区间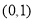 上不可能恒成立,故要使函数
上不可能恒成立,故要使函数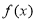 在区间
在区间 上无零点,只要对
上无零点,只要对 ,
,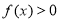 恒成立. 8分
恒成立. 8分
(后续步骤分为解法一和解法二)
解法一:
 ,
,
当 ,即
,即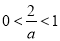 时,由
时,由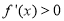 得
得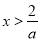 ,由
,由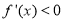 得
得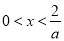 ,
,
即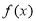 在区间
在区间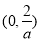 上单调递减,在区间
上单调递减,在区间 上单调递增;
上单调递增;
此时 ,
,
构造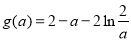 ,
, ,故
,故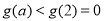 ,
,
所以当 时,
时,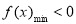 ,即对
,即对 ,
,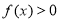 不恒成立,舍去;
不恒成立,舍去;
10分
当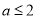 ,即
,即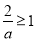 时,由
时,由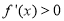 得
得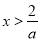 ,由
,由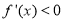 得
得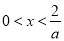 ,
,
即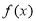 在区间
在区间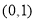 上单调递减,故
上单调递减,故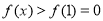 ,
,
满足对 ,
,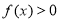 恒成立,
恒成立,
综上,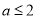 ,即
,即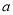 的最大值为2. 12分
的最大值为2. 12分
解法二:
由对 ,
,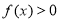 恒成立可得对
恒成立可得对 ,
,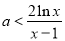 恒成立.
恒成立.
令 ,
,
令 ,由
,由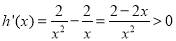 得
得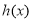 在区间
在区间 上单调递增,
上单调递增,
即 ,从而
,从而 ,
,
即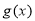 在区间
在区间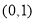 上单调递减,
上单调递减,
由罗比达法则知 ,即
,即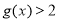 ,
,
若对 ,
,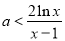 恒成立,可得
恒成立,可得 ,即
,即 的最大值为2 12分
的最大值为2 12分
考点:1、导数在单调性上的应用;2、利用导数求函数的极值、最值.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:高中数学 来源:2015届河南省名校高三上学期期中文科数学试卷(解析版) 题型:解答题
如图所示的多面体中,ABCD是菱形,BDEF是矩形, ED?面ABCD,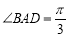 .
.

(1)求证: ;
;
(2)若 .
.
查看答案和解析>>
科目:高中数学 来源:2015届河南省原名校高三上学期第一次摸底考试数学理科数学试卷(解析版) 题型:选择题
已知等差数列 的前n项和为
的前n项和为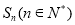 ,且
,且 ,若数列
,若数列 在
在 时为递增数列,则实数
时为递增数列,则实数 的取值范围为( )
的取值范围为( )
A.(-15,+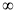 ) B.[-15,+
) B.[-15,+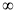 ) C.[-16,+
) C.[-16,+ ) D.(-16,+
) D.(-16,+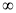 )
)
查看答案和解析>>
科目:高中数学 来源:2015届河南省原名校高三上学期第一次摸底考试数学文科数学试卷(解析版) 题型:填空题
在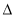 ABC中,
ABC中, ,D是AB边上的一点,
,D是AB边上的一点,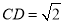 ,△CBD的面积为1,则AC边的长为_______.
,△CBD的面积为1,则AC边的长为_______.
查看答案和解析>>
科目:高中数学 来源:2015届河北省邯郸市高三上学期摸底考试文科数学试卷(解析版) 题型:解答题
为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查得到如下列联表:平均每天喝500ml以上为常喝,体重超过50kg为肥胖。
| 常喝 | 不常喝 | 合计 |
肥胖 |
| 2 |
|
不肥胖 |
| 18 |
|
合计 |
|
| 30 |
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为 。
。
(1)请将上面的列联表补充完整
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由
(3)现从常喝碳酸饮料且肥胖的学生中(2名女生),抽取2人参加电视节目,则正好抽到一男一女的概率是多少?
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: ,其中
,其中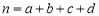 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com