
Ϊ�˽������ͯ�ķ����Ƿ��볣��̼�������й�,�ֶ�30�����꼶ѧ���������ʾ�����õ�����������:ƽ��ÿ���500ml����Ϊ���ȣ����س���50kgΪ���֡�
| ���� | ������ | �ϼ� |
���� |
| 2 |
|
������ |
| 18 |
|
�ϼ� |
|
| 30 |
��֪��ȫ��30���������ȡ1��,�鵽���ֵ�ѧ���ĸ���Ϊ ��
��
��1���뽫�������������������
��2���Ƿ���99��5���İ�����Ϊ�����볣��̼�������йأ�˵���������
��3���ִӳ���̼�������ҷ��ֵ�ѧ���У�2��Ů��������ȡ2�˲μӵ��ӽ�Ŀ�������ó鵽һ��һŮ�ĸ����Ƕ��٣�
�ο����ݣ�
| 0��15 | 0��10 | 0��05 | 0��025 | 0��010 | 0��005 | 0��001 |
| 2��072 | 2��706 | 3��841 | 5��024 | 6��635 | 7��879 | 10��828 |
���ο���ʽ�� ������
������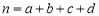 ��
��
��1��
| ���� | ������ | �ϼ� |
���� | 6 | 2 | 8 |
���� | 4 | 18 | 22 |
�ϼ� | 10 | 20 | 30 |
��2����99��5���İ�����Ϊ�����볣��̼�������йأ�
��3��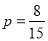 ��
��
��������
�����������1���賣��̼�����Ϸ��ֵ�ѧ����x�ˣ���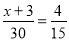 ������
������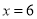 ��
��
��2������֪���ݿ���ã�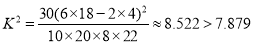 �������жϣ���99��5���İ�����Ϊ�����볣��̼�������йأ�
�������жϣ���99��5���İ�����Ϊ�����볣��̼�������йأ�
��3���賣��̼�����ϵķ���������ΪA��B��C��D��Ů��ΪE��F���á��оٷ���ȷ����ȡ���˵ķ�����15�֣�����һ��һŮ�а��֣�Ӧ�ùŵ�����ʵļ��㹫ʽ���ã�
�����������1���賣��̼�����Ϸ��ֵ�ѧ����x�ˣ�
| ���� | ������ | �ϼ� |
���� | 6 | 2 | 8 |
���� | 4 | 18 | 22 |
�ϼ� | 10 | 20 | 30 |
��2������֪���ݿ���ã�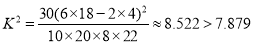
�����99��5���İ�����Ϊ�����볣��̼�������йأ�
��3���賣��̼�����ϵķ���������ΪA��B��C��D��Ů��ΪE��F������ȡ������
AB��AC��AD��AE��AF��BC��BD��BE��BF��CD��CE��CF��DE��DF��EF����15�֡�����һ��һŮ��AE��AF��BE��BF��CE��CF�� DE��DF���ʳ��һ��һŮ�ĸ�����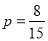
���㣺1��������飻2���ŵ���ͣ�3����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2015�����ʡԭ��У������ѧ�ڵ�һ����������ѧ������ѧ�Ծ��������棩 ���ͣ������
��֪����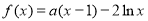 (dΪ������
(d������
��1����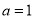 �ԣ���
�ԣ���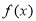 �������䣻
�������䣻
��2��������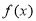 ������(0��1)������㣬��a�����ֵ��
������(0��1)������㣬��a�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�����ʡԭ��У������ѧ�ڵ�һ����������ѧ�Ŀ���ѧ�Ծ��������棩 ���ͣ�ѡ����
������������ȷ���ǣ� ��
A�����⡰ ��ʹ��
��ʹ�� ���ķ��ǡ�
���ķ��ǡ� ������
������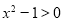 ����
����
B�����⡰�� ����x=y������������������⣺
����x=y������������������⣺
C�����⡱��x=3���� ���ķ������ǡ���
���ķ������ǡ��� ����
���� ����
����
D�����⡰�����ı���ȵ��ı��β��������Ρ��Ǽ����⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015��ӱ�ʡ�����и�����ѧ��������������ѧ�Ծ��������棩 ���ͣ�ѡ����
��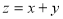 ������
������ ����
���� ����
���� �����ֵΪ6����
�����ֵΪ6���� ����СֵΪ�� ��
����СֵΪ�� ��
A��-5 B��-4 C��-3 D��-2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015��ӱ�ʡ�����и�����ѧ��������������ѧ�Ծ��������棩 ���ͣ�ѡ����
���� ��
�� Ϊ������λ���ڸ�ƽ��������Ӧ�ĵ��ڣ� ��
Ϊ������λ���ڸ�ƽ��������Ӧ�ĵ��ڣ� ��
A����һ���� B���ڶ����� C���������� D����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015��ӱ�ʡ�����и�����ѧ���������Ŀ���ѧ�Ծ��������棩 ���ͣ������
��֪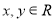 ����
����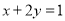 ����
����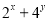 ����Сֵ ��
����Сֵ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015��ӱ�ʡ�����и�����ѧ���������Ŀ���ѧ�Ծ��������棩 ���ͣ�ѡ����
��֪ʵ��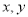 ����
���� ����Ŀ�꺯��
����Ŀ�꺯��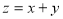 ����СֵΪ�� ��
����СֵΪ�� ��
A��-5 B��-4 C��-3 D��-2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015��ӱ�ʡʯ��ׯ�и߶���ѧ����ĩ����������ѧ�Ծ��������棩 ���ͣ������
����y=x2��1��ֱ��x+y=1Χ�ɵ�ͼ�ε����Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015��ӱ�ʡʯ��ׯ����У�����������ѧ�ڵ�һ���¿��Ŀ���ѧ�Ծ��������棩 ���ͣ������
��10�֣���֪�Ȳ����� ��ǰn���
��ǰn���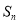 ����
����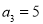 ��
��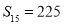
��1��������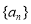 ��ͨ�ʽ��
��ͨ�ʽ��
��2����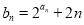 ��������
��������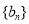 ��ǰn���
��ǰn���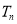 .
.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com