对于在区间
上有意义的两个函数
与
，如果对任意的
，均有
，则称
与
在
上是接近的，否则称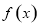
与
在
上是非接近的.现在有两个函数
与
，现给定区间
.
（1）若
，判断
与
是否在给定区间上接近；
（2）是否存在
，使得
与
在给定区间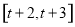
上是接近的；若存在，求
的取值范围；若不存在，请说明理由.
科目：高中数学 来源：2017届河北武邑中学高三理周考11.20数学试卷（解析版） 题型：选择题
已知三棱锥的俯视图与侧视图如图所示，俯视图是边长为2的正三角形，侧视图是有一直角边为2的直角三角形，则该三棱锥的正视图可能为（ ）
查看答案和解析>>
科目：高中数学 来源：2016-2017学年湖南长沙一中高一上学期段测二数学试卷（解析版） 题型：解答题
已知
的三个顶点为
，
，
，求：
（1）过点
与
平行的直线
的方程；
（2）
边垂直平分线
的方程.
查看答案和解析>>
科目：高中数学 来源：2016-2017学年湖南长沙一中高一上学期段测二数学试卷（解析版） 题型：选择题
某工厂生产的
种产品进入某商场销售，商场为吸引厂家第一年免收管理费，因此第一年
种产品定价为每件
元，年销售量为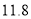
万件，从第二年开始，商场对
种产品征收销售额的
的管理费（即销售
元要征收
元），于是该产品定价每件比第一年增加了
元，预计年销售量减少
万件，要使第二年商场在
种产品经营中收取的管理费不少于
万元，则
的最大值是（ ）
A．
B．
C．
D．
查看答案和解析>>
科目：高中数学 来源：2016-2017学年福建福州外国语高一上期末模拟数学试卷（解析版） 题型：解答题
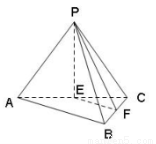
如图，在三棱锥
中，
、
分别为
、
的中点.
(1)求证:
平面
；
(2)若平面
平面
,且
,求证:
平面
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的前
项和
，第
项满足
，则
（ ）
，若
，则实数
的取值范围是（ ）
B．
D．
上的函数
，
是它的导函数，且恒有
成立，则（ ）
B．
D．
在
上为减函数，则实数
的值是 ．