
分析 利用诱导公式、正弦函数的单调性,求得函数y=2sin($\frac{π}{4}$-x)的单调递减区间.
解答 解:函数y=2sin($\frac{π}{4}$-x)=-2sin(x-$\frac{π}{4}$),令2kπ-$\frac{π}{2}$≤x-$\frac{π}{4}$≤2kπ+$\frac{π}{2}$(k∈Z),
求得2kπ-$\frac{π}{4}$≤x≤2kπ+$\frac{3π}{4}$,可得函数的减区间为[2kπ-$\frac{π}{4}$,2kπ+$\frac{3π}{4}$],k∈Z,
故答案为:[2kπ-$\frac{π}{4}$,2kπ+$\frac{3π}{4}$],k∈Z.
点评 本题主要考查诱导公式、正弦函数的单调性,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
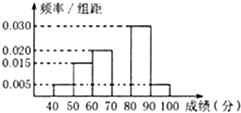 某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如图频率分布直方图(其中分组区间为[40,50),[50,60),…,[90,100]).
某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如图频率分布直方图(其中分组区间为[40,50),[50,60),…,[90,100]).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a⊥b,α∥β,则b⊥β | B. | 若b?β,a⊥b,则α⊥β | C. | 若a⊥b,α⊥β,则b∥β | D. | 若b⊥β,α∥β,则a⊥b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com