
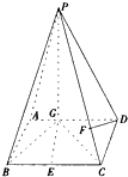
如图,四棱锥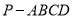 中,底面
中,底面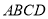 是平行四边形,
是平行四边形,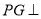 平面
平面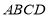 ,垂足为
,垂足为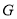 ,
,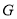 在线段
在线段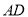 上,
上,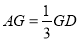 ,
,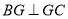 ,
,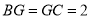 ,
,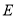 是
是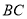 的中点,四面体
的中点,四面体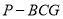 的体积为
的体积为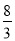 .
.
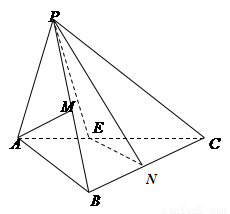
(1)求异面直线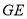 与
与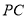 所成角的余弦值;
所成角的余弦值;
(2)棱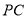 上是否存在一点
上是否存在一点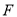 ,使
,使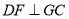 ,若存在,求
,若存在,求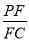 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
科目:高中数学 来源:2016届浙江省高三上学期期中文科数学试卷(解析版) 题型:解答题
如图,三棱锥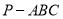 中,
中,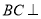 平面
平面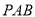 ,
,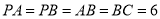 ,点
,点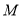 ,
,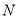 分别为
分别为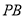 ,
,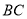 的中点.
的中点.
(1)求证: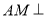 平面
平面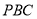 ;
;
(2)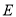 在线段
在线段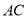 上的点,且
上的点,且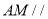 平面
平面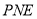 .
.
①确定点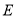 的位置;
的位置;
②求直线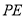 与平面
与平面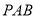 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年浙江省高一4-6班上期中数学卷(解析版) 题型:解答题
已知函数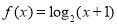 ,当点
,当点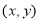 在函数
在函数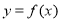 的图象上运动时,点
的图象上运动时,点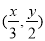 在函数
在函数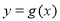 (
(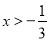 )的图象上运动.
)的图象上运动.
(1)求函数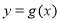 的解析式;
的解析式;
(2)求函数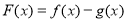 的零点.
的零点.
(3)函数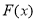 在
在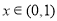 上是否有最大值、最小值;若有,求出最大值、最小值;若没有请说明理由.
上是否有最大值、最小值;若有,求出最大值、最小值;若没有请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年黑龙江齐齐哈尔实验中学高一上期中数学卷(解析版) 题型:选择题
已知函数 若存在实数
若存在实数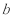 ,使函数
,使函数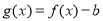 有两个零点,则
有两个零点,则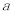 的取值
的取值
范围是( )
A.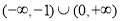
B.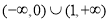
C.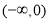
D.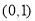
查看答案和解析>>
科目:高中数学 来源:2015-2016学年福建省高二上期中理科数学试卷(解析版) 题型:解答题
某大学毕业生响应国家“自主创业”的号召,今年年初组织一些同学自筹资金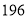 万元购进一台设备,并立即投入生产自行设计的产品,计划第一年维修、保养费用
万元购进一台设备,并立即投入生产自行设计的产品,计划第一年维修、保养费用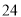 万元,从第二年开始,每年所需维修、保养费用比上一年增加
万元,从第二年开始,每年所需维修、保养费用比上一年增加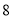 万元,该设备使用后,每年的总收入为
万元,该设备使用后,每年的总收入为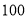 万元,设从今年起使用
万元,设从今年起使用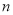 年后该设备的盈利额为
年后该设备的盈利额为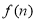 万元。
万元。
(Ⅰ)写出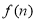 的表达式;
的表达式;
(Ⅱ)求从第几年开始,该设备开始盈利;
(Ⅲ)使用若干年后,对该设备的处理方案有两种:方案一:年平均盈利额达到最大值时,以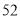 万元价格处理该设备;方案二:当盈利额达到最大值时,以16万元价格处理该设备。问用哪种方案处理较为合算?请说明理由.
万元价格处理该设备;方案二:当盈利额达到最大值时,以16万元价格处理该设备。问用哪种方案处理较为合算?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com