
【题目】如图,直线![]() (
(![]() )关于直线
)关于直线![]() 对称的直线为
对称的直线为![]() ,直线
,直线![]() ,
,![]() 与椭圆
与椭圆![]() 分别交于点A,M和A,N,记直线
分别交于点A,M和A,N,记直线![]() 的斜率为
的斜率为![]() .
.
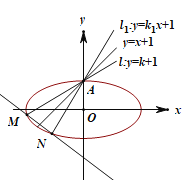
(1)求![]() 的值;
的值;
(2)当![]() 变化时,直线
变化时,直线![]() 是否恒过定点?若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
是否恒过定点?若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
科目:高中数学 来源: 题型:
【题目】已知两圆C1:x2+y2-2x-6y-1=0和C2:x2+y2-10x-12y+45=0.
(1)求证:圆C1和圆C2相交;
(2)求圆C1和圆C2的公共弦所在直线的方程和公共弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:

(1)求分数在[120,130)内的频率;
(2)估计本次考试的中位数;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述中正确的是( )
A. 若![]() ,则“
,则“![]() ”的充要条件是“
”的充要条件是“![]() ”
”
B. 函数![]() 的最大值是
的最大值是![]()
C. 命题“![]() ”的否定是“
”的否定是“![]() ”
”
D. ![]() 是一条直线,
是一条直线,![]() 是两个不同的平面,若
是两个不同的平面,若![]() 则
则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查高一学生在分班选科时是否选择物理科目与性别的关系,随机调查100名高一学生,得到![]() 列联表如下:由此得出的正确结论是( )
列联表如下:由此得出的正确结论是( )
选择物理 | 不选择物理 | 总计 | |
男 | 35 | 20 | 55 |
女 | 15 | 30 | 45 |
总计 | 50 | 50 | 100 |
附: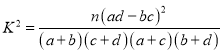
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
A.在犯错误的概率不超过0.01的前提下,认为“选择物理与性别有关”
B.在犯错误的概率不超过0.01的前提下,认为“选择物理与性别无关”
C.有![]() 的把握认为“选择物理与性别有关”
的把握认为“选择物理与性别有关”
D.有![]() 的把握认为“选择物理与性别无关”
的把握认为“选择物理与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角△![]() 中,
中,![]() ,△
,△![]() 通过△
通过△![]() 以直线
以直线![]() 为轴顺时针旋转120°得到(
为轴顺时针旋转120°得到(![]() ),点
),点![]() 为线段
为线段![]() 上一点,且
上一点,且![]() .
.
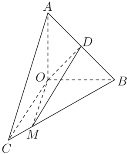
(1)求证:![]() ,并证明:
,并证明:![]() 平面
平面![]() ;
;
(2)分别以![]() 、
、![]() 、
、![]() 为
为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成角的大小(用反余弦运算表示);
所成角的大小(用反余弦运算表示);
(3)若![]() ,求锐二面角
,求锐二面角![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com