
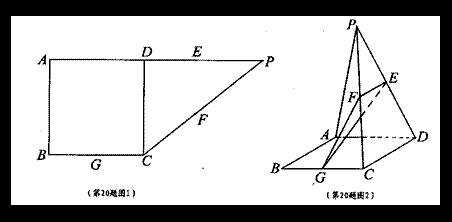
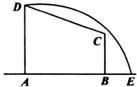
如图所示,在直角梯形ABCP中,AB=BC=3,AP=7,CD⊥AP,现将![]() 沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。
沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。
(I)求证:PA//平面EFG;
(II)若M为线段CD上的一个动点,问当M在什么位置时,MF与平面EFG所成角最大。
(Ⅰ)见解析 (Ⅱ) M为线段CD中点时 ,![]() 最大
最大
方法一: (I)证明:![]() 平面PAD,
平面PAD,
![]() 2分
2分
过P作AD的垂线,垂足为O,则PO![]() 平面ABCD。
平面ABCD。
过O作BC的垂线,交BC于H,以OH,OD,OP为x
轴,y轴,z轴建立空间直角坐标系,
![]() 是二面角P—PC—A的平面角,
是二面角P—PC—A的平面角,![]() ,
,
又![]()
得![]()
![]()
故![]() 4分
4分
设平面EFG的一个法向量为![]() 则
则
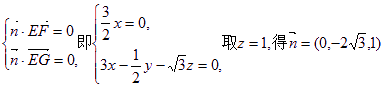 6分
6分
而![]()
![]() 故PA//平面EFG。 7分
故PA//平面EFG。 7分
(II)解:设M(x,2,0),则![]() , 9分
, 9分
设MF与平面EFG所成角为![]() ,
,
则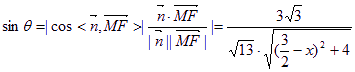 12分
12分
故当![]() 取到最大值,则
取到最大值,则![]() 取到最大值,此时点M为线段CD的中点。14分
取到最大值,此时点M为线段CD的中点。14分
方法二:
(I)证明:取AD的中点H,连结EH,HG。 2分[
![]() H,G为AD,BC的中点,∴HG//CD,又EF//CD。∴EF//HG,
H,G为AD,BC的中点,∴HG//CD,又EF//CD。∴EF//HG,
∴E,F,G,H四点共面
又∵PA//EH,EH![]() 平面EFGH,PA
平面EFGH,PA![]() 平面EFGH,∴PA//平面EFG。 7分
平面EFGH,∴PA//平面EFG。 7分
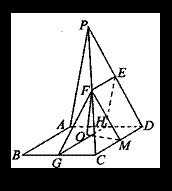
(II)解:过M作MO⊥平面EFG,垂足O,连结OF,
则![]() 即为MF与平面EFG所成角,因为CD//EF,
即为MF与平面EFG所成角,因为CD//EF,
故CD//平面EFG,故CD上的点M到平面EFG的距离
MO为定长,故要使![]() 最大,只要MF最短,故当
最大,只要MF最短,故当
![]() 时,即M为线段CD中点时 ,
时,即M为线段CD中点时 ,![]() 最大。 14分
最大。 14分


科目:高中数学 来源: 题型:
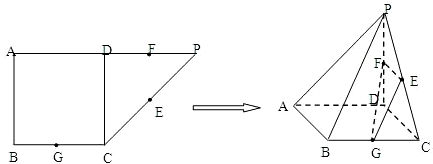
 如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=
如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在直角梯形OABC中,∠COA=∠OAB=
如图所示,在直角梯形OABC中,∠COA=∠OAB=| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
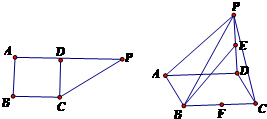 如图所示,在直角梯形ABCP中,AP∥BC,AB⊥AP,AB=BC=3,AP=7,CD⊥AP,现将△PCD沿折线CD折成直二面角P-CD-A,设E,F分别是PD,BC的中点.
如图所示,在直角梯形ABCP中,AP∥BC,AB⊥AP,AB=BC=3,AP=7,CD⊥AP,现将△PCD沿折线CD折成直二面角P-CD-A,设E,F分别是PD,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com