
图
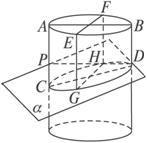
(1)比较EF,GH的大小;
(2)若圆柱的底面半径为r,截面α与母线的夹角为θ,求CD.
科目:高中数学 来源: 题型:
 (2012•茂名二模)如图所示,圆柱的高为2,PA是圆柱的母线,ABCD为矩形,AB=2,BC=4,E、F、G分别是线段PA,PD,CD的中点.
(2012•茂名二模)如图所示,圆柱的高为2,PA是圆柱的母线,ABCD为矩形,AB=2,BC=4,E、F、G分别是线段PA,PD,CD的中点.查看答案和解析>>
科目:高中数学 来源:广东省茂名市2012届高三第二次高考模拟考试数学文科试题 题型:044
如图所示,圆柱的高为2,PA是圆柱的母线,ABCD为矩形,AB=2,BC=4,E、F、G分别是线段PA,PD,CD的中点.
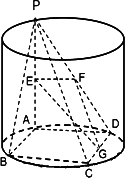
(1)求证:平面PDC⊥平面PAD;
(2)求证:PB//面EFG;
(3)在线段BC上是否存在一点M,使得D到平面PAM的距离为2?若存在,求出BM;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年北京市大兴区高三上学期期末考试理科数学试卷(解析版) 题型:填空题
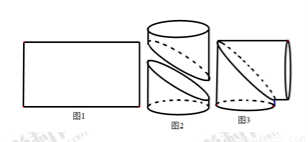
工人师傅在如图1的一块矩形铁皮的中间画了一条曲线,并沿曲线剪开,将所得的两部分卷成圆柱状,如图2,然后将其对接,可做成一个直角的“拐脖”,如图3.对工人师傅所画的曲线,有如下说法
是一段抛物线;
(2)是一段双曲线;
(3)是一段正弦曲线;
(4)是一段余弦曲线;
(5)是一段圆弧.
则正确的说法序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
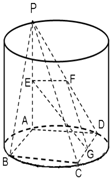 如图所示,圆柱的高为2,PA是圆柱的母线,ABCD为矩形,AB=2,BC=4,E、F、G分别是线段PA,PD,CD的中点.
如图所示,圆柱的高为2,PA是圆柱的母线,ABCD为矩形,AB=2,BC=4,E、F、G分别是线段PA,PD,CD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com