
已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)证明:对任意的 ,存在唯一的
,存在唯一的 ,使
,使 ;
;
(3)设(2)中所确定的 关于
关于 的函数为
的函数为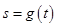 ,证明:当
,证明:当 时,有
时,有 .
.
科目:高中数学 来源: 题型:解答题
(2013•湖北)设n是正整数,r为正有理数.
(1)求函数f(x)=(1+x)r+1﹣(r+1)x﹣1(x>﹣1)的最小值;
(2)证明: ;
;
(3)设x∈R,记[x]为不小于x的最小整数,例如 .令
.令 的值.
的值.
(参考数据: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆 (a>b>0)的左焦为F,右顶点为A,上顶点为B,O为坐标原点,M为椭圆上任意一点,过F,B,A三点的圆的圆心为(p,q).
(a>b>0)的左焦为F,右顶点为A,上顶点为B,O为坐标原点,M为椭圆上任意一点,过F,B,A三点的圆的圆心为(p,q).
(1).当p+q≤0时,求椭圆的离心率的取值范围;
(2).若D(b+1,0),在(1)的条件下,当椭圆的离心率最小时, 的最小值为
的最小值为 ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
判断下列对应是否是从集合A到集合B的函数.
(1) A=B=N*,对应法则f:x→y=|x-3|,x∈A,y∈B;
(2) A=[0,+∞),B=R,对应法则f:x→y,这里y2=x,x∈A,y∈B;
(3) A=[1,8],B=[1,3],对应法则f:x→y,这里y3=x,x∈A,y∈B;
(4) A={(x,y)|x、y∈R},B=R,对应法则:对任意(x,y)∈A,(x,y)→z=x+3y,z∈B.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com