
【题目】候鸟每年都要随季节的变化而进行大规模地迁徙,研究某种鸟类的专家发现,该种鸟类的飞行速度v(单位:m/s)与其耗氧量Q之间的关系为:v=a+blog3 ![]() (其中a,b是实数).据统计,该种鸟类在静止的时候其耗氧量为30个单位,而其耗氧量为90个单位时,其飞行速度为1 m/s.
(其中a,b是实数).据统计,该种鸟类在静止的时候其耗氧量为30个单位,而其耗氧量为90个单位时,其飞行速度为1 m/s.
(1)求出a,b的值;
(2)若这种鸟类为赶路程,飞行的速度不能低于2 m/s,则其耗氧量至少要多少个单位?
【答案】
(1)解:由题意可知,当这种鸟类静止时,它的速度为0 m/s,此时耗氧量为30个单位,故有a+blog3 ![]() =0,
=0,
即a+b=0;①
当耗氧量为90个单位时,速度为1 m/s,
故a+blog3 ![]() =1,整理得a+2b=1.②
=1,整理得a+2b=1.②
解方程组 ![]() 得
得 ![]()
(2)解:由(1)知,v=a+blog3 ![]() =-1+log3
=-1+log3 ![]() .所以要使飞行速度不低于2 m/s,则有v≥2,所以-1+log3
.所以要使飞行速度不低于2 m/s,则有v≥2,所以-1+log3 ![]() ≥2,即log3
≥2,即log3 ![]() ≥3,解得
≥3,解得 ![]() ≥27,即Q≥270.
≥27,即Q≥270.
所以若这种鸟类为赶路程,飞行的速度不能低于2 m/s,则其耗氧量至少要270个单位
【解析】(1)利用该种鸟类在静止的时间其耗氧量为30个单位,而其耗氧量为90个单位时,其飞行速度为1m/s,建立方程组,即可求出a,b的值;
(2)利用飞行的速度不能低于2m/s,建立不等式,即可求出其耗氧量至少要多少个单位.解函数关系未知的应用题
①阅读理解题意
看一看可以用什么样的函数模型,初步拟定函数类型;
②抽象函数模型
在理解问题的基础上,把实际问题抽象为函数模型;
③研究函数模型的性质
根据函数模型,结合题目的要求,讨论函数模型的有关性质,获得函数模型的解;
④得出问题的结论
根据函数模型的解,结合实际问题的实际意义和题目的要求,给出实际问题的解.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:高中数学 来源: 题型:
【题目】如图,在底面为矩形的四棱椎P﹣ABCD中,PB⊥AB.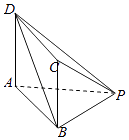
(1)证明:平面PBC⊥平面PCD;
(2)若异面直线PC与BD所成角为60°,PB=AB,PB⊥BC,求二面角B﹣PD﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度v(单位:千克/年)是养殖密度x(单位:尾/立方米)的函数.当x不超过4尾/立方米时,v的值为2千克/年;当4<x≤20时,v是x的一次函数,当x达到20尾/立方米时,因缺氧等原因,v的值为0千克/年.
(1)当0<x≤20时,求函数v关于x的函数表达式;
(2)当养殖密度x为多大时,鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地一年的气温Q(t)(单位:℃)与时间t(月份)之间的关系如图所示,已知该年的平均气温为10 ℃,令C(t)表示时间段[0,t]的平均气温,下列四个函数图象中,最能表示C(t)与t之间的函数关系的是( )
A.
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确命题的个数是( ) ①对于命题p:x∈R,使得x2+x+1<0,则¬p:x∈R,均有x2+x+1>0;
②命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题;
③回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为 ![]() =1.23x+0.08;
=1.23x+0.08;
④m=3是直线(m+3)x+my﹣2=0与直线mx﹣6y+5=0互相垂直的充要条件.
A.1
B.3
C.2
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《孙子算经》中有如下问题:“今有三女,长女五日一归,中女四日一归,少女三日一归.问:三女何日相会?” 意思是:“一家出嫁的三个女儿中,大女儿每五天回一次娘家,二女儿每四天回一次娘家,小女儿每三天回一次娘家.三个女儿从娘家同一天走后,至少再隔多少天三人再次相会?”假如回娘家当天均回夫家,若当地风俗正月初二都要回娘家,则从正月初三算起的一百天内,有女儿回娘家的天数有( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系 ![]() 中,圆
中,圆 ![]() 的参数方程为
的参数方程为 ![]() (
( ![]() 为参数,
为参数, ![]() 是大于0的常数).以坐标原点为极点,
是大于0的常数).以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)求圆 ![]() 的极坐标方程和圆
的极坐标方程和圆 ![]() 的直角坐标方程;
的直角坐标方程;
(2)分别记直线 ![]() :
: ![]() ,
, ![]() 与圆
与圆 ![]() 、圆
、圆 ![]() 的异于原点的焦点为
的异于原点的焦点为 ![]() ,
, ![]() ,若圆
,若圆 ![]() 与圆
与圆 ![]() 外切,试求实数
外切,试求实数 ![]() 的值及线段
的值及线段 ![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com