
【题目】随着互联网的迅速发展,越来越多的消费者开始选择网络购物这种消费方式某营销部门统计了2019年某月锦州的十大特产的网络销售情况得到网民对不同特产的最满意度![]() 和对应的销售额
和对应的销售额![]() (万元)数据,如下表:
(万元)数据,如下表:
特产种类 | 甲 | 乙 | 丙 | 丁 | 戊 | 已 | 庚 | 辛 | 壬 | 癸 |
最满意度 |
|
|
|
|
|
|
|
|
|
|
销售额 |
|
|
|
|
|
|
|
|
|
|
![]() 求销量额
求销量额![]() 关于最满意度
关于最满意度![]() 的相关系数
的相关系数![]() ;
;
![]() 我们约定:销量额
我们约定:销量额![]() 关于最满意度
关于最满意度![]() 的相关系数
的相关系数![]() 的绝对值在
的绝对值在![]() 以上(含
以上(含![]() )是线性相关性较强;否则,线性相关性较弱.如果没有达到较强线性相关,则采取“末位淘汰”制(即销售额最少的特产退出销售),并求在剔除“末位淘汰”的特产后的销量额
)是线性相关性较强;否则,线性相关性较弱.如果没有达到较强线性相关,则采取“末位淘汰”制(即销售额最少的特产退出销售),并求在剔除“末位淘汰”的特产后的销量额![]() 关于最满意度
关于最满意度![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() ).
).
参考数据:![]()
![]() ,
,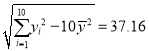 ,
,![]() ,
,![]() .
.
附:对于一组数据![]() .其回归直线方程
.其回归直线方程![]() 的斜率和截距的最小二乘法估计公式分别为:
的斜率和截距的最小二乘法估计公式分别为: ,
,![]() .线性相关系数
.线性相关系数
 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和Sn满足Sn+1=a2Sn+a1 , 其中a2≠0.
(1)求证:{an}是首项为1的等比数列;
(2)若a2>﹣1,求证 ![]() ,并给出等号成立的充要条件.
,并给出等号成立的充要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1. 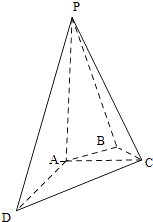
(1)证明:PC⊥AD;
(2)求二面角A﹣PC﹣D的正弦值;
(3)设E为棱PA上的点,满足异面直线BE与CD所成的角为30°,求AE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为R的半球O的底面圆O在平面α内,过点O作平面α的垂线交半球面于点A,过圆O的直径CD作平面α成45°角的平面与半球面相交,所得交线上到平面α的距离最大的点为B,该交线上的一点P满足∠BOP=60°,则A、P两点间的球面距离为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为6的正方形![]() 中,弧
中,弧![]() 的圆心为
的圆心为![]() ,过弧
,过弧![]() 上的点
上的点![]() 作弧
作弧![]() 的切线,与
的切线,与![]() 、
、![]() 分别相交于点
分别相交于点![]() 、
、![]() ,
,![]() 的延长线交
的延长线交![]() 边于点
边于点![]() .
.
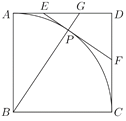
(1)设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数解析式,并写出函数定义域;
之间的函数解析式,并写出函数定义域;
(2)当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com