
【题目】已知抛物线的参数方程为 ![]() (t为参数),其中p>0,焦点为F,准线为l.过抛物线上一点M作l的垂线,垂足为E.若|EF|=|MF|,点M的横坐标是3,则p= .
(t为参数),其中p>0,焦点为F,准线为l.过抛物线上一点M作l的垂线,垂足为E.若|EF|=|MF|,点M的横坐标是3,则p= .
【答案】2
【解析】解:抛物线的参数方程为 ![]() (t为参数),其中p>0,焦点为F,准线为l,消去参数可得x=2p
(t为参数),其中p>0,焦点为F,准线为l,消去参数可得x=2p ![]() ,
,
化简可得y2=2px,表示顶点在原点、开口向右、对称轴是x轴的抛物线,
故焦点F( ![]() ,0),准线l的方程为x=﹣
,0),准线l的方程为x=﹣ ![]() .
.
则由抛物线的定义可得|ME|=|MF|,再由|EF|=|MF|,可得△MEF为等边三角形.
设点M的坐标为(3,m ),则点E(﹣ ![]() ,m).
,m).
把点M的坐标代入抛物线的方程可得m2=2×p×3,即 p= ![]() .
.
再由|EF|=|ME|,可得 p2+m2= ![]() ,即 p2+6p=9+
,即 p2+6p=9+ ![]() +3p,解得p=2,或p=﹣6 (舍去),
+3p,解得p=2,或p=﹣6 (舍去),
所以答案是 2.
【考点精析】本题主要考查了抛物线的参数方程的相关知识点,需要掌握抛物线![]() 的参数方程可表示为
的参数方程可表示为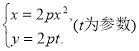 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】设椭圆E: ![]() 的焦点在x轴上
的焦点在x轴上
(1)若椭圆E的焦距为1,求椭圆E的方程;
(2)设F1 , F2分别是椭圆E的左、右焦点,P为椭圆E上第一象限内的点,直线F2P交y轴于点Q,并且F1P⊥F1Q,证明:当a变化时,点P在某定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个命题与正整数n有关,如果当![]() 时命题成立,那么可推得当
时命题成立,那么可推得当![]() 时命题也成立. 现已知当n=8时该命题不成立,那么可推得 ( )
时命题也成立. 现已知当n=8时该命题不成立,那么可推得 ( )
A. 当n=7时该命题不成立 B. 当n=7时该命题成立
C. 当n=9时该命题不成立 D. 当n=9时该命题成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:

则下面结论中不正确的是
A. 新农村建设后,种植收入减少
B. 新农村建设后,其他收入增加了一倍以上
C. 新农村建设后,养殖收入增加了一倍
D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高三年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图:
分组 | 频数 | 频率 |
|
|
|
| 24 |
|
| 4 | 0.1 |
| 2 | 0.05 |
合计 |
| 1 |
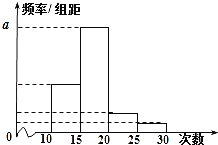
(1)求出表中![]() ,
,![]() 及图中
及图中![]() 的值;
的值;
(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间![]() 内的人数;
内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关统计知识的四个命题正确的是( )
A. 衡量两变量之间线性相关关系的相关系数![]() 越接近
越接近![]() ,说明两变量间线性关系越密切
,说明两变量间线性关系越密切
B. 在回归分析中,可以用卡方![]() 来刻画回归的效果,
来刻画回归的效果,![]() 越大,模型的拟合效果越差
越大,模型的拟合效果越差
C. 线性回归方程对应的直线![]() 至少经过其样本数据点中的一个点
至少经过其样本数据点中的一个点
D. 线性回归方程![]() 中,变量
中,变量![]() 每增加一个单位时,变量
每增加一个单位时,变量![]() 平均增加
平均增加![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
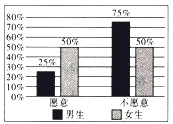
【题目】某组织在某市征集志愿者参加志愿活动,现随机抽出60名男生和40名女生共100人进行调查,统计出100名市民中愿意参加志愿活动和不愿意参加志愿活动的男女生比例情况,具体数据如图所示.
(1)根据条件完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为愿意参与志愿活动与性别有关?
的把握认为愿意参与志愿活动与性别有关?
愿意 | 不愿意 | 总计 | |
男生 | |||
女生 | |||
总计 |
(2)现用分层抽样的方法从愿意参加志愿活动的市民中选取7名志愿者,再从中抽取2人作为队长,求抽取的2人至少有一名女生的概率.
参考数据及公式:
|
|
|
|
|
|
|
|
|
|
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制.各等级划分标准见下表.
内,发布成绩使用等级制.各等级划分标准见下表.
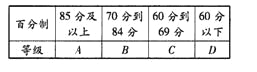
规定:![]() 三级为合格等级,D为不合格等级.为了解该校高一年级学生身体素质情况,从中抽取了
三级为合格等级,D为不合格等级.为了解该校高一年级学生身体素质情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计.按照
名学生的原始成绩作为样本进行统计.按照![]() 的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示.
的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示.
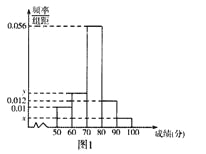
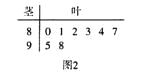
(I)求![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值,并估计该校高一年级学生成绩是合格等级的概率;
的值,并估计该校高一年级学生成绩是合格等级的概率;
(II)在选取的样本中,从![]() 两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是
两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是![]() 等级的概率.
等级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com