
分析 (1)求出f(x)的表达式,求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)问题转化为a<$\frac{1}{x}$-$\frac{1}{ln(1+x)}$在x∈(0,1]恒成立,令q(x)=$\frac{1}{x}$-$\frac{1}{ln(1+x)}$,x∈(0,1],根据函数的单调性求出g(x)的最小值,从而求出a的范围即可.
解答 解:(1)当a=-$\frac{1}{3}$时,
f(x)=$\frac{1}{3}$ln(x+1)+$\frac{2}{3(x+1)}$-$\frac{2}{3}$=$\frac{2}{3}$[2ln(x+1)+$\frac{1}{x+1}$-1],(x>-1),
令p(x)=2ln(x+1)+$\frac{1}{x+1}$-1,(x>-1),
p′(x)=$\frac{2x+1}{{(x+1)}^{2}}$,
令p′(x)>0,解得:x>-$\frac{1}{2}$,令p′(x)<0,解得:-1<x<-$\frac{1}{2}$,
∴p(x)在(-1,-$\frac{1}{2}$)递减,在(-$\frac{1}{2}$,+∞)递增,
即f(x)在(-1,-$\frac{1}{2}$)递减,在(-$\frac{1}{2}$,+∞)递增;
(2)函数g(x)=(1-ax)ln(1+x)-x,
若对任意x∈(0,1]都有g(x)>0成立,
即a<$\frac{1}{x}$-$\frac{1}{ln(1+x)}$在x∈(0,1]恒成立,
令q(x)=$\frac{1}{x}$-$\frac{1}{ln(1+x)}$,x∈(0,1],
q′(x)=$\frac{(x+1{)[ln(x+1)]}^{2}{+x}^{2}}{{x}^{2}(x+1{)[ln(x+1)]}^{2}}$,
令m(x)=(x+1)[ln(x+1)]2+x2,x∈(0,1],
m′(x)=ln(x+1)[ln(x+1)+2]+2x,x∈(0,1],
∴m′(x)>0,
∴m(x)在(0,1]递增,m(x)max=m(1)=-1+$\frac{1}{{2(ln2)}^{2}}$<0,
∴q′(x)<0在(0,1]恒成立,
∴q(x)在(0,1]递减,
∴q(x)min=q(1)=1-$\frac{1}{ln2}$,
∴a<1-$\frac{1}{ln2}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,AB为⊙O的直径,点C在⊙O上,PA⊥平面ABC,点E为线段PB的中点.
如图所示,AB为⊙O的直径,点C在⊙O上,PA⊥平面ABC,点E为线段PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${∫}_{0}^{5}$(2x2-4)dx | B. | ${∫}_{0}^{π}$$\frac{1}{2}$sinxdx | C. | ${∫}_{1}^{3}$$\frac{1}{x}$dx | D. | ${∫}_{0}^{\frac{π}{2}}$2cosxdx |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
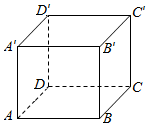
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
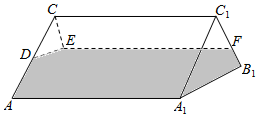 如图,一个侧棱长为l的直三棱柱ABC-A1B1C1容器中盛有液体(不计容器厚度).若液面恰好分别过棱AC,BC,B1C1,A1Cl的中点D,E,F,G.
如图,一个侧棱长为l的直三棱柱ABC-A1B1C1容器中盛有液体(不计容器厚度).若液面恰好分别过棱AC,BC,B1C1,A1Cl的中点D,E,F,G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com