
| A. | ${∫}_{0}^{5}$(2x2-4)dx | B. | ${∫}_{0}^{π}$$\frac{1}{2}$sinxdx | C. | ${∫}_{1}^{3}$$\frac{1}{x}$dx | D. | ${∫}_{0}^{\frac{π}{2}}$2cosxdx |
分析 分别根据定积分的计算法则计算即可.
解答 解:${∫}_{0}^{5}$(2x2-4)dx=($\frac{2}{3}$x3-4x)|${\;}_{0}^{5}$=$\frac{2}{3}$×125-20≠1,
${∫}_{0}^{π}$$\frac{1}{2}$sinxdx=-$\frac{1}{2}$cosx|${\;}_{0}^{π}$=-$\frac{1}{2}$(-1-1)=1,
${∫}_{1}^{3}$$\frac{1}{x}$dx=lnx|${\;}_{1}^{3}$=ln3≠1,
${∫}_{0}^{\frac{π}{2}}$2cosxdx=2sinx|${\;}_{0}^{\frac{π}{2}}$=2,
故选:B.
点评 本题考查了定积分的计算,关键是求出原函数,属于基础题.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R(x0≠0),x0+$\frac{1}{{x}_{0}}$≤2 | B. | ?x0∈R(x0≠0),x0+$\frac{1}{{x}_{0}}$<2 | ||
| C. | ?x∈R(x≠0),x+$\frac{1}{x}$≤2 | D. | ?x∈R(x≠0),x+$\frac{1}{x}$<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{13}{25}$ | C. | $\frac{38}{75}$ | D. | $\frac{81}{125}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
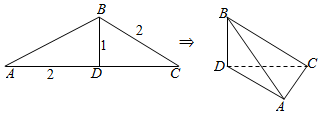
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
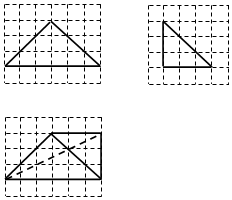
| A. | 9 | B. | $\frac{27}{2}$ | C. | 18 | D. | 27 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com