
【题目】定义:若无穷数列![]() 满足
满足![]() 是公比为
是公比为![]() 的等比数列,则称数列
的等比数列,则称数列![]() 为“
为“![]() 数列”.设数列
数列”.设数列![]() 中
中![]()
(1)若![]() ,且数列
,且数列![]() 是“
是“![]() 数列”,求数列
数列”,求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,请判断数列
,请判断数列![]() 是否为“
是否为“![]() 数列”,并说明理由;
数列”,并说明理由;
(3)若数列![]() 是“
是“![]() 数列”,是否存在正整数
数列”,是否存在正整数![]() ,使得
,使得![]() ?若存在,请求出所有满足条件的正整数
?若存在,请求出所有满足条件的正整数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1)![]() ;(2)是“
;(2)是“![]() 数列”,证明见解析;(3)存在,
数列”,证明见解析;(3)存在,![]() ;
;
【解析】
(1)计算![]() ,故
,故![]() 是公比为1的等比数列,计算得到答案.
是公比为1的等比数列,计算得到答案.
(2)![]() 是“
是“![]() ”数列,化简得到
”数列,化简得到![]() ,即
,即![]() ,得到证明.
,得到证明.
(3)![]() 是公比为2的等比数列,
是公比为2的等比数列,![]() ,利用累加法得到
,利用累加法得到![]() ,得到
,得到![]() ,计算得到答案.
,计算得到答案.
(1)由题意可得![]() ,
,
由数列![]() 为“
为“![]() 数列”可得
数列”可得![]() ,即
,即![]() ,
,
则![]() 是公比为1的等比数列,即
是公比为1的等比数列,即![]() ,
,
则![]() 是首项为1,公差为3的等差数列,
是首项为1,公差为3的等差数列,![]() ;
;
(2)![]() 是“
是“![]() ”数列,,
”数列,,
理由如下:![]() 时,由
时,由![]() ,可得
,可得![]() ,
,
两式作差可得![]() 即
即![]() ,
,
则![]() ,两式作差可得
,两式作差可得![]() ,即
,即![]() ,
,
由![]() ,可得
,可得![]() ,则
,则![]() ,
,
则![]() 对任意
对任意![]() 成立,则
成立,则![]() 为首项是
为首项是![]() ,公比为3的等比软列,
,公比为3的等比软列,
则![]() 为
为![]() 数列;
数列;
(3)由![]() 是
是![]() 数列,可得
数列,可得![]() 是公比为2的等比数列,
是公比为2的等比数列,
即![]() ,则
,则![]() ,由
,由![]() ,可得
,可得![]() ,则
,则![]() ,
,
则![]() ,
,
则![]() ,若正整数
,若正整数![]() 满足
满足![]() ,则
,则![]() ,
,
由![]() ,则
,则![]() ,则
,则![]() ,
,
若![]() ,则
,则![]() ,不满足
,不满足![]() ,
,
若![]() ,则
,则![]() ,则
,则![]() ,即
,即![]() ,
,
则![]() ,则正整数
,则正整数![]() ,则
,则![]() ;
;
因此存在满足条件的![]() .
.


科目:高中数学 来源: 题型:
【题目】已知某校甲、乙、丙三个兴趣小组的学生人数分别为36,24,12.现采用分层抽样的方法从中抽取6人,进行睡眠质量的调查.
(1)应从甲、乙、丙三个兴趣小组的学生中分别抽取多少人?
(2)设抽出的6人分别用![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 表示,现从6人中随机抽取2人做进一步的身体检查.
表示,现从6人中随机抽取2人做进一步的身体检查.
(i)试用所给字母列出所有可能的抽取结果;
(ii)设![]() 为事件“抽取的2人来自同一兴趣小组”,求事件
为事件“抽取的2人来自同一兴趣小组”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,圆![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线
轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 是
是![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
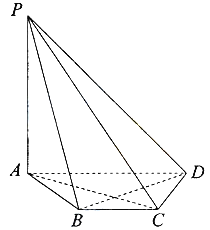
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
(Ⅰ)证明:BD⊥PC;
(Ⅱ)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】明初出现了一大批杰出的骑兵将领,比如徐达、常遇春、李文忠、蓝玉和朱棣.明初骑兵军团击败了不可一世的蒙古骑兵,是当时世界上最强骑兵军团.假设在明军与元军的某次战役中,明军有8位将领,善用骑兵的将领有5人;元军有8位将领,善用骑兵的有4人.
(1)现从明军将领中随机选取4名将领,求至多有3名是善用骑兵的将领的概率;
(2)在明军和元军的将领中各随机选取2人,![]() 为善用骑兵的将领的人数,写出
为善用骑兵的将领的人数,写出![]() 的分布列,并求
的分布列,并求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn,若对任意正整数n,总存在正整数m,使得Sn=am,则称数列{an}为S数列.
(1)S数列的任意一项是否可以写成其某两项的差?请说明理由.
(2)①是否存在等差数列为S数列,若存在,请举例说明;若不存在,请说明理由.
②是否存在正项递增等比数列为S数列,若存在,请举例说明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从0,1,2,3,4这五个数中任选三个不同的数组成一个三位数,记X为所组成的三位数各位数字之和.
(1)求X是奇数的概率;
(2)求X的概率分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com