
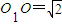 ,A、B是圆O1上两点,若∠AO1B=
,A、B是圆O1上两点,若∠AO1B=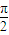 ,则A,B两点间的球面距离为 .
,则A,B两点间的球面距离为 .  ,OA=OB=2
,OA=OB=2 ,又∠AO1B=
,又∠AO1B=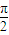



 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源:2011年云南省昆明市高三复习5月适应性检测数学试卷(理科)(解析版) 题型:填空题
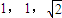 ,若三个小圆所在的平面两两垂直且公共点为P则OP= .
,若三个小圆所在的平面两两垂直且公共点为P则OP= .查看答案和解析>>
科目:高中数学 来源:2011年湖北省华师一附中、荆州中学高考数学模拟试卷(理科)(解析版) 题型:解答题
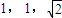 ,若三个小圆所在的平面两两垂直且公共点为P则OP= .
,若三个小圆所在的平面两两垂直且公共点为P则OP= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com