
(本题满分10分)在 中,已知角
中,已知角 所对的边分别是
所对的边分别是 ,边
,边 ,且
,且 ,又
,又 的面积为
的面积为 ,求
,求 的值.
的值.
a+b=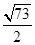 。
。
【解析】本试题主要是考查了解三角形和两角和差公式的综合运用。
先根据已知化简得到tan(A+B)= 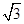 ,所以C=
,所以C=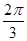 ,然后利用正弦面积公式得到△ABC的面积为S△ABC=
,然后利用正弦面积公式得到△ABC的面积为S△ABC=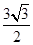 ,∴
,∴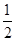 absinC=
absinC=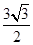 即
即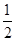 ab×
ab×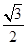 =
=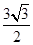 ,得到ab=6,再结合余弦定理得到a+b=
,得到ab=6,再结合余弦定理得到a+b=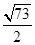 。
。
解: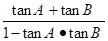 =
=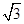 ,即tan(A+B)=
,即tan(A+B)= 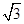
∴tan(π-C)= 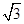 , ∴-tanC=
, ∴-tanC=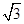 ,∴C=
,∴C=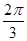
又△ABC的面积为S△ABC=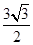 ,∴
,∴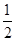 absinC=
absinC=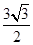 即
即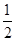 ab×
ab×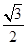 =
=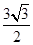 , ∴ab=6
, ∴ab=6
又由余弦定理可得c2=a2+b2-2abcosC
∴(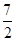 )2= a2+b2-2abcos
)2= a2+b2-2abcos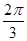 ∴(
∴(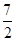 )2= a2+b2+ab=(a+b)2-ab∴(a+b)2=
)2= a2+b2+ab=(a+b)2-ab∴(a+b)2=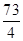 ,
,
∵a+b>0, ∴a+b=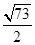


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:高中数学 来源:2012-2013学年辽宁省丹东市高三上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分10分)
在直角坐标系xoy中,以o为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为 ,M,N分别为C与x轴,y轴的交点
,M,N分别为C与x轴,y轴的交点
(1)写出C的直角坐标方程,并求出M,N的极坐标;
(2)设MN的中点为P,求直线OP的极坐标方程.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省石家庄市高三暑期第二次考试理科数学试卷(解析版) 题型:解答题
(本题满分10分)在平面直角坐标系 中,
中, .
.
(1)求以线段 为邻边的平行四边形的两条对角线的长;
为邻边的平行四边形的两条对角线的长;
(2)设实数 满足
满足 ,求
,求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com