
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)设![]() ,若
,若![]() ,
,![]() 为函数
为函数![]() 的两个不同极值点,证明:
的两个不同极值点,证明:![]() .
.
【答案】(1)见解析(2)见解析
【解析】
(1)求出原函数的导函数![]() ,可得
,可得![]() 时,若
时,若![]() ,
,![]() ,
,![]() 单调递增;若
单调递增;若![]() ,求出导函数的零点,根据导函数与0的关系可得原函数的单调性;(2)根据导数先得
,求出导函数的零点,根据导函数与0的关系可得原函数的单调性;(2)根据导数先得![]() 在R上单调递增,原题转化为证
在R上单调递增,原题转化为证![]() ,根据
,根据![]() 和
和![]() 进一步转化为证
进一步转化为证![]() ,再由
,再由![]() ,得到证明
,得到证明![]() ,设
,设![]() ,
,![]() ,化为证明
,化为证明![]() ,设
,设![]() ,利用导数证明
,利用导数证明![]() 即可.
即可.
解:(1)![]() ,
,
若![]() ,
,![]() ,
,![]() ,
,![]() 单调递增.
单调递增.
若![]() ,由
,由![]() ,解得
,解得![]() ,
,
且![]() ,
,![]() ,
,![]() 单调递减,
单调递减,
![]() ,
,![]() ,
,![]() 单调递增.
单调递增.
综上,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,
,
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)![]() ,
,
故![]() 在
在![]() 上单调递增,即证:
上单调递增,即证:![]() ,
,
也即证:![]() ,
,
又![]()
![]() ,
,
![]() ,
,
所以![]() ,
,![]() 为方程
为方程![]() 的两根,
的两根,
即![]()
即证![]() ,即
,即![]() ,
,
而①-②得![]() ,
,
即证:![]() ,
,
不妨设![]() ,
,![]() ,
,
则证:![]() 变形得
变形得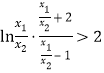 ,
,
所以![]() ,
,![]() ,
,
设![]() ,
,
则![]() ,
,
∴![]() 在
在![]() 单调递增,
单调递增,
![]() ,
,
即结论成立.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M: ![]() 及其上一点A(2,4)
及其上一点A(2,4)

(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;
(3)设点T(t,o)满足:存在圆M上的两点P和Q,使得![]() ,求实数t的取值范围。
,求实数t的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的右焦点为
的右焦点为![]() ,离心率
,离心率![]() .
.
(1)求椭圆C的标准方程;
(2)已知动直线l过点F,且与椭圆C交于A,B两点,试问x轴上是否存在定点M ,使得![]() 恒成立?若存在,求出点M的坐标,若不存在,请说明理由.
恒成立?若存在,求出点M的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)(注意:在试题卷上作答无效)
如图,四棱锥S-ABCD中,SD![]() 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD![]() DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC
DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC![]() 平面SBC .
平面SBC .
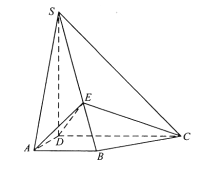
(Ⅰ)证明:SE=2EB;
(Ⅱ)求二面角A-DE-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果从北大打车到北京车站去接人,聪明的专家一定会选择走四环。虽然从城中间直穿过去看上去很诱人,但考虑到北京的道路几乎总是正南正北的方向,事实上不会真有人认为这样走能抄近路。在城市中,专家估算两点之间的距离时,不会直接去测量两点之间的直线距离,而会去考虑它们相距多少个街区。在理想模型中,假设每条道路都是水平或者竖直的,那么只要你朝着目标走(不故意绕远路),不管你这样走,花费的路程都是一样的。出租车几何学(taxicab geometry),所谓的“出租车几何学”是由十九世纪的另一位真专家赫尔曼-闵可夫斯基所创立的。在出租车几何学中,点还是形如![]() 的有序实数对,直线还是满足
的有序实数对,直线还是满足![]() 的所有
的所有![]() 组成的图形,角度大小的定义也和原来一样。只是直角坐标系内任意两点
组成的图形,角度大小的定义也和原来一样。只是直角坐标系内任意两点![]() ,
,![]() 定义它们之间的一种“距离”:
定义它们之间的一种“距离”:![]() ,请解决以下问题:
,请解决以下问题:
(1)定义:“圆”是所有到定点“距离”为定值的点组成的图形,求“圆周”上的所有点到点![]() 的“距离”均为
的“距离”均为![]() 的“圆”方程,并作出大致图像;
的“圆”方程,并作出大致图像;
(2)在出租车几何学中,到两点![]() 、
、![]() “距离”相等的点的轨迹称为线段
“距离”相等的点的轨迹称为线段![]() 的“垂直平分线”,已知点
的“垂直平分线”,已知点![]() ,
,![]() ,
,![]() ;
;
①写出在线段![]() 的“垂直平分线”的轨迹方程,并写出大致图像;
的“垂直平分线”的轨迹方程,并写出大致图像;
②求证:![]() 三边的“垂直平分线”交于一点(该点称为
三边的“垂直平分线”交于一点(该点称为![]() 的“外心”),并求出
的“外心”),并求出![]() 的“外心”.
的“外心”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就.在“杨辉三角”中,第![]() 行的所有数字之和为
行的所有数字之和为![]() ,若去除所有为1的项,依次构成数列
,若去除所有为1的项,依次构成数列![]() ,则此数列的前55项和为( )
,则此数列的前55项和为( )

A. 4072B. 2026C. 4096D. 2048
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求满足下列条件的椭圆的标准方程:
(1)焦点在y轴上,焦距是4,且经过点M(3,2);
(2)c∶a=5∶13,且椭圆上一点到两焦点的距离的和为26.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com