练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知在区间上的值域.

    (1)求的值；

    (2)若不等式在上恒成立，求实数的取值范围；

    (3)若函数有三个零点，求实数的取值范围.

    【答案】（1）（2）（3）

    【解析】

    试题（1）对 配方，求出对称轴 ，讨论若 三种情况，由单调性可得最小值，解方程，即可得到所求 的值；
    （2）由题意可得 ，化为 ，令 ，求出的范围，求得右边函数的最小值即可得到的范围；
    （3）令 ，可化为| 有3个不同的实根．令 ，讨论的范围和单调性， 有两个不同的实数 已知函数有3个零点等价为 或 ，由二次函数图象可得不等式组，解不等式可得 的范围．

    试题解析：（1） ，满足条件；

    ，综上

    （2）

    则

    （3）问题等价于 有三个不同的根，令，所以方程 有两个不同的解 ，且，因此

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知a+b=1，对a，b∈（0，+∞）， + ≥|2x﹣1|﹣|x+1|恒成立，
    （1）求 + 的最小值；
    （2）求x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C的对边分别为a，b，c，满足2acosB=2c﹣b．
    （1）求角A；
    （2）若△ABC的面积为 ，且a= ，请判断△ABC的形状，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|x﹣2|．
    （1）解不等式f（x）+f（x+1）≥5；
    （2）若|a|＞1且 ，证明：|b|＞2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率是，短轴的一个端点到右焦点的距离为，直线与椭圆交于两点．

    （1）求椭圆的方程；

    （2）当实数变化时，求的最大值；

    （3）求面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

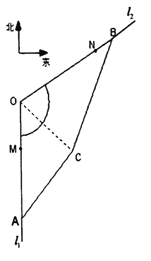
    【题目】已知分别是海岸线上的三个集镇， 位于的正南方向处， 位于的北偏东60°方向处；

    （1）为了缓解集镇的交通压力，拟在海岸线上分别修建码头，开辟水上直达航线，使， .勘测时发现以为圆心， 为半径的扇形区域为浅水区，不适宜船只航行，问此航线是否影响船只航行？

    （2）为了发展经济需要，政府计划填海造陆，建造一个商业区（如图四边形所示），其中， ， ，求该商业区的面积的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（且）.

    （1）当时，函数恒有意义，求实数的取值范围；

    （2）是否存在这样的实数，使得函数在区间上为减函数，并且最大值为1？如果存在，试求出的值；如果不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数满足，且．

    求函数的解析式；

    求在区间上的最大值和最小值；

    当时，恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从一堆产品正品与次品都多于2件中任取2件，观察正品件数和次品件数，则下列说法：

    “恰好有1件次品”和“恰好2件都是次品”是互斥事件

    “至少有1件正品”和“全是次品”是对立事件

    “至少有1件正品”和“至少有1件次品”是互斥事件但不是对立事件

    “至少有1件次品”和“全是正品”是互斥事件也是对立事件

    其中正确的有______填序号．

    查看答案和解析>>

    同步练习册答案