
【题目】已知函数![]() (
(![]() 且
且![]() ).
).
(1)当![]() 时,函数
时,函数![]() 恒有意义,求实数
恒有意义,求实数![]() 的取值范围;
的取值范围;
(2)是否存在这样的实数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上为减函数,并且最大值为1?如果存在,试求出
上为减函数,并且最大值为1?如果存在,试求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出![]() 盒该产品获利润
盒该产品获利润![]() 元;未售出的产品,每盒亏损
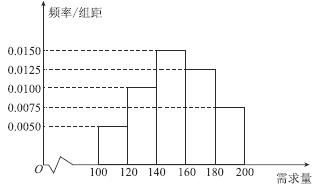
元;未售出的产品,每盒亏损![]() 元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了
元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了![]() 盒该产品,以
盒该产品,以![]() (单位:盒,
(单位:盒, ![]() )表示这个开学季内的市场需求量,(单位:元)表示这个开学季内经销该产品的利润.
)表示这个开学季内的市场需求量,(单位:元)表示这个开学季内经销该产品的利润.
(1)根据直方图估计这个开学季内市场需求量![]() 的中位数;
的中位数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计利润不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,以原点为圆心,以椭圆
,以原点为圆心,以椭圆![]() 的短半轴长为半径的圆与直线
的短半轴长为半径的圆与直线![]() 相切. 过点
相切. 过点![]() 的直线与椭圆
的直线与椭圆![]() 相交于
相交于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() ,求直线的方程;
,求直线的方程;
(3)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地建一座桥,两端的桥墩已建好,这两墩相距![]() 米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为
米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为![]() 米的相邻两墩之间的桥面工程费用为
米的相邻两墩之间的桥面工程费用为![]() 万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为
万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为![]() 万元. 假设需要新建n个桥墩.
万元. 假设需要新建n个桥墩.
(1)写出n关于![]() 的函数关系式;
的函数关系式;
(2)试写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)当![]() =640米时,需新建多少个桥墩才能使
=640米时,需新建多少个桥墩才能使![]() 最小?
最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出.若每辆车的月租金每增加50元,未租出的车将会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定位3600元时,能租出多少辆车?
(2)当每辆车的月租金定位多少元时,租赁公司的月收益最大,最大月收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班有学生60人,现将所有学生按1,2, 3,…,60随机编号,若采用系统抽样的方法抽取一个容量为4的样本(等距抽样),已知编号为3, 33, 48号学生在样本中,则样本中另一个学生的编号为( )
A. 28 B. 23 C. 18 D. 13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com