
【题目】某地建一座桥,两端的桥墩已建好,这两墩相距![]() 米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为
米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为![]() 米的相邻两墩之间的桥面工程费用为
米的相邻两墩之间的桥面工程费用为![]() 万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为
万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为![]() 万元. 假设需要新建n个桥墩.
万元. 假设需要新建n个桥墩.
(1)写出n关于![]() 的函数关系式;
的函数关系式;
(2)试写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)当![]() =640米时,需新建多少个桥墩才能使
=640米时,需新建多少个桥墩才能使![]() 最小?
最小?
科目:高中数学 来源: 题型:
【题目】已知直线![]() ,半径为2的圆
,半径为2的圆![]() 与
与![]() 相切,圆心
相切,圆心![]() 在
在![]() 轴上且在直线
轴上且在直线![]() 的右上方.
的右上方.
(1)求圆的方程;
(2)若直线过点![]() 且与圆
且与圆![]() 交于
交于![]() 两点(
两点(![]() 在
在![]() 轴上方,
轴上方,![]() 在
在![]() 轴下方),问在
轴下方),问在![]() 轴正半轴上是否存在定点
轴正半轴上是否存在定点![]() ,使得
,使得![]() 轴平分
轴平分![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若用斜二测画法把一个高为10 cm的圆柱的底面画在x′O′y′平面上,则该圆柱的高应画成( )
A. 平行于z′轴且长度为10 cm
B. 平行于z′轴且长度为5 cm
C. 与z′轴成45°且长度为10 cm
D. 与z′轴成45°且长度为5 cm
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 且
且![]() ).
).
(1)当![]() 时,函数
时,函数![]() 恒有意义,求实数
恒有意义,求实数![]() 的取值范围;
的取值范围;
(2)是否存在这样的实数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上为减函数,并且最大值为1?如果存在,试求出
上为减函数,并且最大值为1?如果存在,试求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】五一节期间,某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置, 指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见右下表.
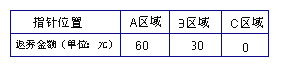

例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(1)已知顾客甲消费后获得![]() 次转动转盘的机会,已知他每转一次转盘指针落在区域边界的概率为
次转动转盘的机会,已知他每转一次转盘指针落在区域边界的概率为![]() ,每次转动转盘的结果相互独立,设
,每次转动转盘的结果相互独立,设![]() 为顾客甲转动转盘指针落在区域边界的次数,
为顾客甲转动转盘指针落在区域边界的次数,![]() 的数学期望
的数学期望![]() ,方差
,方差![]() .求
.求![]() 、
、![]() 的值;
的值;
(2)顾客乙消费280元,并按规则参与了活动,他获得返券的金额记为![]() (元).求随机变量
(元).求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
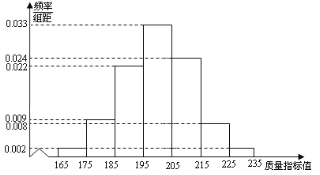
【题目】从某企业的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
(Ⅰ)求这500件产品质量指标值的样本平均数![]() 和样本方差
和样本方差![]() (用同一组数据用该区间的中点值用代表);
(用同一组数据用该区间的中点值用代表);
(Ⅱ)由频率分布直方图可以认为,这种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)利用该正态分布,求![]() ;
;
(ii)某用户从该企业购买了100件这种产品,记![]() 表示这100件产品中质量指标值位于区间
表示这100件产品中质量指标值位于区间![]() 的产品件数,利用(i)的结果,求
的产品件数,利用(i)的结果,求![]() .
.
附:![]() ,若
,若![]() ,则
,则![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答下列各题:
(1)在△ABC中,已知C=45°,A=60°,b=2,求此三角形最小边的长及a与B的值;
(2)在△ABC中,已知A=30°,B=120°,b=5,求C及a与c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com