
【题目】若圆x2+y2﹣4x﹣4y﹣10=0上至少有三个不同点到直线l:ax+by=0的距离为 ![]() .则直线l的倾斜角的取值范围是 .
.则直线l的倾斜角的取值范围是 .
【答案】[ ![]() ,
, ![]() ]
]
【解析】解:圆x2+y2﹣4x﹣4y﹣10=0化简为标准方程,可得(x﹣2)2+(y﹣2)2=18,
∴圆心坐标为C(2,2),半径r=3 ![]() ,
,
∵在圆上至少有三个不同的点到直线l:ax+by=0的距离为 ![]() ,
,
∴圆心到直线的距离应小于或等于r﹣ ![]() =
= ![]() ,
,
由点到直线的距离公式,得 ![]()
![]() ,
,
∴(2a+2b)2≤2(a2+b2),整理得 ![]() ,
,
解之得2﹣ ![]() ≤
≤ ![]() ≤2+
≤2+ ![]() ,
,
∵直线l:ax+by=0的斜率k=﹣ ![]() ∈[2﹣
∈[2﹣ ![]() ,2+
,2+ ![]() ]
]
∴设直线l的倾斜角为α,则tanα∈[2﹣ ![]() ,2+
,2+ ![]() ],即tan
],即tan ![]() ≤tanα≤tan
≤tanα≤tan ![]() .
.
由此可得直线l的倾斜角的取值范围是[ ![]() ,
, ![]() ].
].
所以答案是:[ ![]() ,
, ![]() ]
]
【考点精析】掌握直线的倾斜角是解答本题的根本,需要知道当直线l与x轴相交时, 取x轴作为基准, x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角.特别地,当直线l与x轴平行或重合时, 规定α=0°.


科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E、F、G、H分别为AA1、AB、BB1、B1C1的中点,则异面直线EF与GH所成的角等于( ) 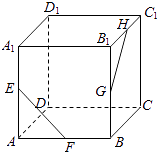
A.45°
B.60°
C.90°
D.120°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体A﹣BCD,则在四面体ABCD中,下列结论正确的是( ) 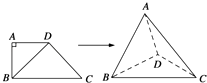
A.平面ABD⊥平面ABC
B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC
D.平面ADC⊥平面ABC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,内角A,B,C所对的边分别为a,b,c,已知 ![]() a=2csinA.
a=2csinA.
(1)求角C的值;
(2)若c= ![]() ,且S△ABC=
,且S△ABC= ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,定直线
,定直线![]() :
: ![]() ,动圆
,动圆![]() 过点
过点![]() ,且与直线
,且与直线![]() 相切.
相切.
(Ⅰ)求动圆![]() 的圆心轨迹
的圆心轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线与曲线
的直线与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,分别过点
两点,分别过点![]() ,
, ![]() 作曲线
作曲线![]() 的切线
的切线![]() ,
, ![]() ,两条切线相交于点
,两条切线相交于点![]() ,求
,求![]() 外接圆面积的最小值.
外接圆面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市某矿山企业生产某产品的年固定成本为![]() 万元,每生产千件该产品需另投入
万元,每生产千件该产品需另投入![]() 万元,设该企业年内共生产此种产品
万元,设该企业年内共生产此种产品![]() 千件,并且全部销售完,每千件的销售收入为
千件,并且全部销售完,每千件的销售收入为![]() 万元,且
万元,且
(Ⅰ)写出年利润![]() (万元)关于产品年产量
(万元)关于产品年产量![]() (千件)的函数关系式;
(千件)的函数关系式;
(Ⅱ)问:年产量![]() 为多少千件时,该企业生产此产品所获年利润最大?
为多少千件时,该企业生产此产品所获年利润最大?
注:年利润=年销售收入-年总成本.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com