解:①由x≠0得,即函数的定义域为(-∞,0)∪(0,+∞)关于原点对称,且f(-x)=
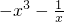
=-f(x),故函数是奇函数.
②由

得,x=

,则定义域为
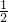
不关于原点对称.该函数不具有奇偶性.
③定义域为R,关于原点对称,且f(-x)=x
4-x≠x
4+x,f(-x)=x
4-x≠-(x
4+x),故其不具有奇偶性.
④定义域为R,关于原点对称,
当x>0时,f(-x)=-(-x)
2-2=-(x
2+2)=-f(x);
当x<0时,f(-x)=(-x)
2+2=-(-x
2-2)=-f(x);
当x=0时,f(0)=0;故该函数为奇函数.
分析:①根据分母不为零求出函数的定义域,先判断是否关于原点对称,再验证f(-x)与-f(x)的关系,最后下结论;
②根据偶次被开方数大于等于零求出函数的定义域,判断出不关于原点对称,再下结论;
③由解析式不受任何限制求出定义域为R,再验证f(-x)与-f(x)的关系,最后下结论;
④将解析式中的范围并在一起求出定义域为R,再分类讨论x>0时和x<0时f(-x)与-f(x)的关系,注意x的范围代入对应的关系式,最后下结论.
点评:本题考查了函数的奇偶性判断方法,先由解析式求出求出函数的定义域并判断是否关于原点对称,若不对称再下结论;否则,验证f(-x)与-f(x)的关系,最后下结论.

 ;
;  ;
; .
.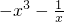 =-f(x),故函数是奇函数.
=-f(x),故函数是奇函数. 得,x=
得,x= ,则定义域为
,则定义域为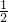 不关于原点对称.该函数不具有奇偶性.
不关于原点对称.该函数不具有奇偶性.
