
(本题满分10分)选修4 - 5 :不等式选讲
设函数,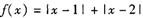 .
.
(I)求证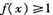 ;
;
(II)若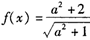 成立,求x的取值范围.
成立,求x的取值范围.
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:解答题
如图,某小区拟在空地上建一个占地面积为2400平方米的矩形休闲广场,按照设计要求,休闲广场中间有两个完全相同的矩形绿化区域,周边及绿化区域之间是道路(图中阴影部分),道路的宽度均为2米.怎样设计矩形休闲广场的长和宽,才能使绿化区域的总面积最大?并求出其最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某商品进货价每件50元,据市场调查,当销售价格(每件x元)为50<x≤80时,每
天售出的件数为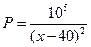 ,若要使每天获得的
,若要使每天获得的 利润最多,销售价格每件应定为多少元
利润最多,销售价格每件应定为多少元 ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com