
若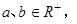 求证:
求证: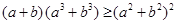 .
.
科目:高中数学 来源: 题型:解答题
如图,已知小矩形花坛ABCD中,AB=3 m,AD=2 m,现要将小矩形花坛建成大矩形花坛AMPN,使点B在AM上,点D在AN上,且对角线MN过点C.
(1)要使矩形AMPN的面积大于32 m2,AN的长应在什么范围内?
(2)M,N是否存在这样的位置,使矩形AMPN的面积最小?若存在,求出这个最小面积及相应的AM,AN的长度;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了降低能源损耗,某体育馆的外墙需要建造隔热层.体育馆要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度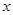 (单位:cm)满足关系:
(单位:cm)满足关系: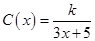 (
(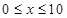 ,
,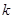 为常数),若不建隔热层,每年能源消耗费用为8万元.设
为常数),若不建隔热层,每年能源消耗费用为8万元.设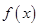 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求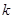 的值及
的值及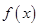 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用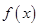 达到最小?并求最小值.
达到最小?并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
老峰镇计划建造一个室内面积为800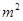 的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1
的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1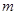 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3 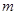 宽的空地。当矩形温室的边长各为多少时?蔬菜的种植面积最大。最大种植面积是多少?
宽的空地。当矩形温室的边长各为多少时?蔬菜的种植面积最大。最大种植面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com