练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    老峰镇计划建造一个室内面积为800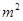的矩形蔬菜温室。在温室内，沿左．右两侧与后侧内墙各保留1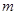宽的通道，沿前侧内墙保留3 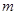宽的空地。当矩形温室的边长各为多少时？蔬菜的种植面积最大。最大种植面积是多少？

    当矩形温室的左侧边长为，后侧边长为时，蔬菜的种植面积最大，最大种植面积为.

    解析试题分析：设出矩形的长为与宽，建立蔬菜面积关于矩形边长的函数关系式＝，再利用基本不等式变形求解．
    试题解析：设矩形温室的左侧边长为，后侧边长为，蔬菜的种植面积，则.
    蔬菜的种植面积 
    所以  
    当
    答：当矩形温室的左侧边长为，后侧边长为时，蔬菜的种植面积最大，最大种植面积为.
    考点：基本不等式的实际应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    若求证： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知焦点在y轴,顶点在原点的抛物线C1经过点P(2,2),以C1上一点C2为圆心的圆过定点A(0,1),记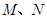为圆与轴的两个交点.
    (1)求抛物线的方程;
    (2)当圆心在抛物线上运动时,试判断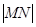是否为一定值？请证明你的结论;
    (3)当圆心在抛物线上运动时,记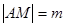,,求的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知正数a、b、c满足abc＝1，求证：(a＋2)(b＋2)(c＋2)≥27.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数f(x)＝.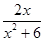
    (1)若f(x)>k的解集为{x|x<－3，或x>－2}，求k的值；
    (2)对任意x>0，f(x)≤t恒成立，求t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    如图，某小区拟在空地上建一个占地面积为2400平方米的矩形休闲广场，按照设计要求，休闲广场中间有两个完全相同的矩形绿化区域，周边及绿化区域之间是道路（图中阴影部分），道路的宽度均为2米．怎样设计矩形休闲广场的长和宽，才能使绿化区域的总面积最大？并求出其最大面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知不等式2｜x－3｜＋｜x－4｜＜2a．
    （Ⅰ）若a＝1，求不等式的解集；
    （Ⅱ）若已知不等式的解集不是空集，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    设变量x，y满足约束条件，则目标函数z=x2+y2的取值范围是（　　）

    A． B． C．( 1 , 16 ) D． 

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    点在直线上移动时，的最小值为         

    查看答案和解析>>

    同步练习册答案