
为了降低能源损耗,某体育馆的外墙需要建造隔热层.体育馆要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度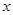 (单位:cm)满足关系:
(单位:cm)满足关系: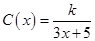 (
(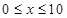 ,
,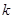 为常数),若不建隔热层,每年能源消耗费用为8万元.设
为常数),若不建隔热层,每年能源消耗费用为8万元.设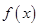 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求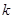 的值及
的值及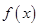 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用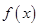 达到最小?并求最小值.
达到最小?并求最小值.
(1)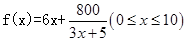 ;(2)即隔热层修建
;(2)即隔热层修建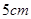 厚时,总费用
厚时,总费用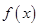 达到最小,最小值为70万元.
达到最小,最小值为70万元.
解析试题分析:(1)由建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系: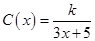 (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.我们可得C(0)=8,得k=40,进而得到C(x)=
(0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.我们可得C(0)=8,得k=40,进而得到C(x)= .建造费用为C1(x)=6x,则根据隔热层建造费用与20年的能源消耗费用之和为f(x),我们不难得到f(x)的表达式.
.建造费用为C1(x)=6x,则根据隔热层建造费用与20年的能源消耗费用之和为f(x),我们不难得到f(x)的表达式.
(2)由(1)中所求的f(x)的表达式,我们利用导数法,求出函数f(x)的单调性,然后根据函数单调性易求出总费用f(x)的最小值.
(1)当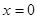 时,
时,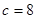 ,
,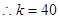 ,
,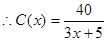 2分
2分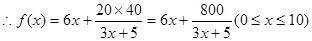 5分
5分
(2)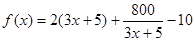 , 7分
, 7分
设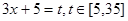 ,
, .
.
当且仅当 这时
这时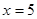 ,因此
,因此 的最小值为70.
的最小值为70.
即隔热层修建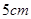 厚时,总费用
厚时,总费用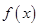 达到最小,最小值为70万元. 10分
达到最小,最小值为70万元. 10分
考点:函数模型的选择与应用;函数最值的应用;利用导数求闭区间上函数的最值.


科目:高中数学 来源: 题型:解答题
某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由形状为长方形A1B1C1D1的休闲区和环公园人行道(阴影部分)组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米(如图所示).
(1)若设休闲区的长和宽的比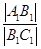 =x(x>1),求公园ABCD所占面积S关于x的函数S(x)的解析式;
=x(x>1),求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)要使公园所占面积最小,则休闲区A1B1C1D1的长和宽该如何设计?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知焦点在y轴,顶点在原点的抛物线C1经过点P(2,2),以C1上一点C2为圆心的圆过定点A(0,1),记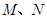 为圆
为圆 与
与 轴的两个交点.
轴的两个交点.
(1)求抛物线 的方程;
的方程;
(2)当圆心 在抛物线上运动时,试判断
在抛物线上运动时,试判断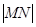 是否为一定值?请证明你的结论;
是否为一定值?请证明你的结论;
(3)当圆心 在抛物线上运动时,记
在抛物线上运动时,记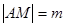 ,
, ,求
,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,某小区拟在空地上建一个占地面积为2400平方米的矩形休闲广场,按照设计要求,休闲广场中间有两个完全相同的矩形绿化区域,周边及绿化区域之间是道路(图中阴影部分),道路的宽度均为2米.怎样设计矩形休闲广场的长和宽,才能使绿化区域的总面积最大?并求出其最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某商品进货价每件50元,据市场调查,当销售价格(每件x元)为50<x≤80时,每
天售出的件数为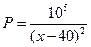 ,若要使每天获得的
,若要使每天获得的 利润最多,销售价格每件应定为多少元
利润最多,销售价格每件应定为多少元 ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com