Question

12．已知椭圆C的中心在坐标原点，焦点在x轴上，左顶点为A，左焦点为F₁（-2，0），点B（2，$\sqrt{2}$）在椭圆C上，直线y=kx（k≠0）与椭圆C交于E，F两点，直线AE，AF分别与y轴交于点M，N
（Ⅰ）求椭圆C的方程；
（Ⅱ）在x轴上是否存在点P，使得无论非零实数k怎样变化，总有∠MPN为直角？若存在，求出点P的坐标，若不存在，请说明理由．

Answer 1

分析 （Ⅰ）由题意可设椭圆标准方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），结合已知及隐含条件列关于a，b，c的方程组，求解方程组得到a²，b²的值，则椭圆方程可求；
（Ⅱ）设F（x₀，y₀），E（-x₀，-y₀），写出AE、AF所在直线方程，求出M、N的坐标，得到以MN为直径的圆的方程，由圆的方程可知以MN为直径的圆经过定点（±2，0），即可判断存在点P．

解答 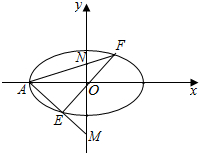解：（Ⅰ）由题意可设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），
则c=2，a²-b²=c²，$\frac{4}{{a}^{2}}$+$\frac{2}{{b}^{2}}$=1，解得：a²=8，b²=4．
可得椭圆C的方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1；
（Ⅱ）如图，设F（x₀，y₀），E（-x₀，-y₀），则$\frac{{{x}_{0}}^{2}}{8}$+$\frac{{{y}_{0}}^{2}}{4}$=1，A（-2$\sqrt{2}$，0），
AF所在直线方程y=$\frac{{y}_{0}}{{x}_{0}+2\sqrt{2}}$（x+2$\sqrt{2}$），
取x=0，得y=$\frac{2\sqrt{2}{y}_{0}}{{x}_{0}+2\sqrt{2}}$，
∴N（0，$\frac{2\sqrt{2}{y}_{0}}{{x}_{0}+2\sqrt{2}}$），
AE所在直线方程为y=$\frac{{y}_{0}}{{x}_{0}-2\sqrt{2}}$（x+2$\sqrt{2}$），
取x=0，得y=$\frac{2\sqrt{2}{y}_{0}}{{x}_{0}-2\sqrt{2}}$．
则以MN为直径的圆的圆心坐标为（0，$\frac{-2\sqrt{2}{x}_{0}{y}_{0}}{8-{{x}_{0}}^{2}}$），
半径r=$\frac{4{y}_{0}}{8-{{x}_{0}}^{2}}$，
圆的方程为x²+（y-$\frac{-2\sqrt{2}{x}_{0}{y}_{0}}{8-{{x}_{0}}^{2}}$）²=$\frac{16{{y}_{0}}^{2}}{（8-{{x}_{0}}^{2}）^{2}}$=$\frac{16}{{{y}_{0}}^{2}}$，即x²+（y+$\frac{\sqrt{2}{x}_{0}}{{y}_{0}}$）²=$\frac{16}{{{y}_{0}}^{2}}$．
取y=0，得x=±2．
可得以MN为直径的圆经过定点（±2，0）．
可得在x轴上存在点P（±2，0），
使得无论非零实数k怎样变化，总有∠MPN为直角．

点评 本题考查椭圆的方程和简单性质，考查直线与圆位置关系的应用，考查整体运算思想方法，是中档题．