
 ax2-(a-1)x,(a∈R).
ax2-(a-1)x,(a∈R). ;②曲线C在点M处的切线平行于直线AB,则称函数f(x)=存在“中值相依切线”.
;②曲线C在点M处的切线平行于直线AB,则称函数f(x)=存在“中值相依切线”. x2,抛物线的顶点为O(0,0),即函数y=g(x)的零点为0,不在原点右侧,不满足条件.(2分)
x2,抛物线的顶点为O(0,0),即函数y=g(x)的零点为0,不在原点右侧,不满足条件.(2分) ax2-(a-1)x=
ax2-(a-1)x= a(x-
a(x- )2-
)2- ,抛物线开口向上且过原点,对称轴
,抛物线开口向上且过原点,对称轴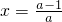 <0,所以抛物线与x轴的另一交点在对称轴的左侧,故函数y=g(x)的零点不在原点右侧,不满足条件.(3分)
<0,所以抛物线与x轴的另一交点在对称轴的左侧,故函数y=g(x)的零点不在原点右侧,不满足条件.(3分) ax2-(a-1)x=
ax2-(a-1)x= a(x-
a(x- )2-
)2- ,抛物线开口向上且过原点,对称轴
,抛物线开口向上且过原点,对称轴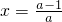 >0,所以抛物线与x轴的另一交点在对称轴的右侧,故函数y=g(x)有一个零点在原点右侧,满足条件.(4分)
>0,所以抛物线与x轴的另一交点在对称轴的右侧,故函数y=g(x)有一个零点在原点右侧,满足条件.(4分) ax2-(a-1)x=
ax2-(a-1)x= a(x-
a(x- )2-
)2- ,抛物线开口向下且过原点,对称轴
,抛物线开口向下且过原点,对称轴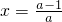 >0,所以抛物线与x轴的另一交点在对称轴的右侧,故函数y=g(x)有一个零点在原点右侧,满足条件.(5分)
>0,所以抛物线与x轴的另一交点在对称轴的右侧,故函数y=g(x)有一个零点在原点右侧,满足条件.(5分) a
a +(a-1)x1,y2=lnx2-
+(a-1)x1,y2=lnx2- a
a +(a-1)x2.
+(a-1)x2.
 a(x1+x2)+(a-1)(8分)
a(x1+x2)+(a-1)(8分) ,(9分)
,(9分)
 a(x1+x2)+(a-1)=
a(x1+x2)+(a-1)= .
. =
= ,即
,即 =
= .(11分)
.(11分) =t(t>1),上式化为:lnt=2-
=t(t>1),上式化为:lnt=2- ,即lnt+
,即lnt+ =2.(12分)
=2.(12分) ,则h′(t)=
,则h′(t)= .
. =2成立.
=2成立.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2(x-1) |
| x+1 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| a |
| ||
| x |
| 6 |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com