练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】（12分）如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．

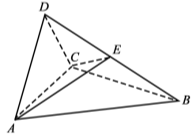
    （1）证明：平面ACD⊥平面ABC；

    （2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D–AE–C的余弦值．

    【答案】

    （1）见解析

    （2）二面角的余弦值为.

    【解析】

    （1）由题设可得，

    又是直角三角形，所以

    取AC的中点O，连接DO,BO,则DO⊥AC,DO=AO

    又由于

    所以

    （2）

    由题设及（1）知，两两垂直，以为坐标原点，的方向为轴正方向，为单位长，建立如图所示的空间直角坐标系，则

    由题设知，四面体ABCE的体积为四面体ABCD的体积的，从而E到平面ABC的距离为D到平面ABC的距离的，即E为DB的中点，得E.故

    设是平面DAE的法向量，则

    可取

    设是平面AEC的法向量，则同理可得

    则

    所以二面角D-AE-C的余弦值为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知矩形ABCD中，AB=2，AD=1，M为CD的中点．如图将△ADM沿AM折起，使得平面ADM⊥平面ABCM．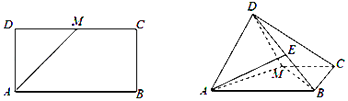
    （1）求证：BM⊥平面ADM；
    （2）若点E是线段DB上的中点，求三棱锥E﹣ABM的体积V1与四棱锥D﹣ABCM的体积V2之比．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】计算题
    （1）已知cos（ +x）= ，（ ＜x＜ ），求 的值．
    （2）若 ， 是夹角60°的两个单位向量，求 =2 + 与 =﹣3 +2 的夹角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}、{bn}满足：a1= ，an+bn=1，bn+1= ．
    （1）求a2 ， a3；
    （2）证数列{ }为等差数列，并求数列{an}和{bn}的通项公式；
    （3）设Sn=a1a2+a2a3+a3a4+…+anan+1 ， 求实数λ为何值时4λSn＜bn恒成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若把函数y=sin（ωx﹣ ）的图象向左平移 个单位，所得到的图象与函数y=cosωx的图象重合，则ω的一个可能取值是（ ）
    A.2
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|x2﹣1|﹣2a+3，下列五个结论：
    ①当 时，函数f（x）没有零点；
    ②当 时，函数f（x）有两个零点；
    ③当 时，函数f（x）有四个零点；
    ④当a=2时，函数f（x）有三个零点；
    ⑤当a＞2时，函数f（x）有两个零点．
    其中正确的结论的序号是 ． （填上所有正确结论的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数有极值，且导函数的极值点是的零点。（极值点是指函数取极值时对应的自变量的值）

    求b关于a的函数关系式，并写出定义域；

    证明：b>3a;

    若， 这两个函数的所有极值之和不小于，求a的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数y=sin（ωx+φ）（ω＞0，|φ|＜ ）在同一个周期内，当x= 时y取最大值1，当x= 时y取最小值﹣1．
    （1）求函数的解析式y=f（x）；
    （2）当x∈[ ， ]时．求函数y=f（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，已知角A，B，C所对的三条边分别是a，b，c，且 ．
    （1）求角B的大小；
    （2）若 ，求△ABC的面积．

    查看答案和解析>>

    同步练习册答案