
【题目】已知矩形ABCD中,AB=2,AD=1,M为CD的中点.如图将△ADM沿AM折起,使得平面ADM⊥平面ABCM. 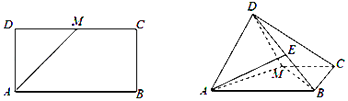
(1)求证:BM⊥平面ADM;
(2)若点E是线段DB上的中点,求三棱锥E﹣ABM的体积V1与四棱锥D﹣ABCM的体积V2之比.
【答案】
(1)证明:因为矩形ABCD中,AB=2,AD=1,M为CD的中点,
所以 ![]() ,所以AM2+BM2=AB2,所以BM⊥AM.
,所以AM2+BM2=AB2,所以BM⊥AM.
因为平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,
又BM平面ABCM,且BM⊥AM,
∴BM⊥平面ADM.
(2)解:因为E为DB的中点,所以 ![]() ,
,
又直角三角形ABM的面积 ![]() ,
,
梯形ABCM的面积 ![]() ,
,
所以 ![]() ,且
,且 ![]() ,
,
所以 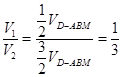
【解析】(1)推导出BM⊥AM,BM⊥AM,由此能证明BM⊥平面ADM.(2)推导出 ![]() ,
, ![]() ,且
,且 ![]() ,由此能求出三棱锥E﹣ABM的体积V1与四棱锥D﹣ABCM的体积V2之比.
,由此能求出三棱锥E﹣ABM的体积V1与四棱锥D﹣ABCM的体积V2之比.
【考点精析】根据题目的已知条件,利用直线与平面垂直的判定的相关知识可以得到问题的答案,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,已知下列条件解三角形:
①A=60°,a= ![]() ,b=1;
,b=1;
②A=30°,a=1,b=2;
③A=30°,c=10,a=6;
④A=30°,c=10,a=5,
其中有唯一解的序号为( )
A.①②③
B.①②④
C.②③④
D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
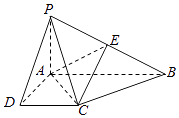
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AD⊥AB,DC∥AB,PA=1,AB=2,PD=BC= ![]() .
. 
(1)求证:平面PAD⊥平面PCD;
(2)试在棱PB上确定一点E,使截面AEC把该几何体分成的两部分PDCEA与EACB的体积比为2:1;
(3)在(2)的条件下,求二面角E﹣AC﹣P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在实数集R上的函数,且y=f(x+1)是偶函数,当x≥1时,f(x)=2x﹣1,则f( ![]() ),f(
),f( ![]() ),f(
),f( ![]() )的大小关系是( )
)的大小关系是( )
A.f( ![]() )<f(
)<f( ![]() )<f(
)<f( ![]() )
)
B.f( ![]() )<f(
)<f( ![]() )<f(
)<f( ![]() )??
)??
C.f( ![]() )<f(
)<f( ![]() )<f(
)<f( ![]() )
)
D.f( ![]() )<f(
)<f( ![]() )<f(
)<f( ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盒中共有形状大小完全相同的5个球,其中有2个红球和3个白球.若从中随机取2个球,则概率为 ![]() 的事件是( )
的事件是( )
A.都不是红球
B.恰有1个红球
C.至少有1个红球
D.至多有1个红球
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2ax+5(a>1).
(1)若f(x)的定义域和值域均是[1,a],求实数a的值;
(2)若对任意的x1 , x2∈[1,a+1],总有|f(x1)﹣f(x2)|≤4,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
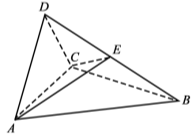
(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com