
| A. | y=x-1和y=$\root{3}{{(x-1)}^{3}}$ | B. | y=$\frac{{x}^{4}-1}{{x}^{2}-1}$和y=x2+1 | ||
| C. | y=${3}^{{log}_{3}x}$和y=$\sqrt{{x}^{2}}$ | D. | y=$\sqrt{{x}^{2}}$和y=x |
分析 分别判断两个函数的定义域和对应法则是否一致即可
解答 解:∵y=$\root{3}{{(x-1)}^{3}}$=x-1的定义域是R,两个函数的定义域和对应法则完全相同,∴表示同一函数的.
对应B,y=$\frac{{x}^{4}-1}{{x}^{2}-1}$的定义域是{x|x≠±1},y=x2+1的定义域的R,两函数的定义域不同,故不表示同一函数;
对应C,y=${3}^{{log}_{3}x}$的定义域是(0,+∞)和y=$\sqrt{{x}^{2}}$的定义域是R,两函数的定义域不同,故不表示同一函数;
对应D,y=$\sqrt{{x}^{2}}$=|x|与y=x的解析式不同,故不表示同一函数,
故选A.
点评 本题主要考查判断函数是否为同一函数,判断的依据主要是判断两个函数的定义域和定义法则是否一致即可


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
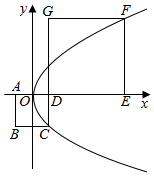 如图,正方形ABCD中,坐标原点O为AD的中点,正方形DEFG的边长为b,若D为抛物线y2=2ax(0<a<b)的焦点,且此抛物线经过C,F两点,则$\frac{b}{a}$=1+$\sqrt{2}$.
如图,正方形ABCD中,坐标原点O为AD的中点,正方形DEFG的边长为b,若D为抛物线y2=2ax(0<a<b)的焦点,且此抛物线经过C,F两点,则$\frac{b}{a}$=1+$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 年份 | 2013 | 2014 | 2015 | 2016 |
| 年份代号(x) | 1 | 2 | 3 | 4 |
| PM2.5指数(y) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 钝角△ | B. | Rt△ | C. | 等边△ | D. | 等腰Rt△ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com