
【题目】如图所示,某桥是抛物线形拱桥,当水面在l时,拱顶离水面2 m,水面宽4 m.
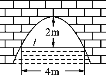
(1)水位下降1 m后,计算水面宽多少米?
(2)已知经过上述抛物线焦点且斜率为2的直线交抛物线于A、B两点,求A、B两点间的距离![]() .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出![]() 与销售额
与销售额![]() (单位:万元)具有较强的相关性,且两者之间有如下对应数据:
(单位:万元)具有较强的相关性,且两者之间有如下对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 28 | 36 | 52 | 56 | 78 |
(1)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)中的线性回归方程,当广告费支出为10万元时,预测销售额是多少?
参考数据: ![]() ,
,![]() ,
,![]() 。
。
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两人约定在20∶00到21∶00之间相见,并且先到者必须等迟到者40分钟方可离去,如果两人出发是各自独立的,在20∶00至21∶00各时刻相见的可能性是相等的,则他们两人在约定时间内相见的概率为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米两斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=4(单位:升),则输入k的值为( )

A. 10 B. 12 C. 14 D. 16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的一个焦点
的一个焦点![]() 与抛物线
与抛物线![]() 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为![]() .
.
(1)求该椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,且点
两点,且点![]() 恰为弦
恰为弦![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某果农选取一片山地种植红柚,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:![]() ),获得的所有数据按照区间
),获得的所有数据按照区间![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,得到频率分布直方图如图。已知样本中产量在区间
进行分组,得到频率分布直方图如图。已知样本中产量在区间![]() 上的果树株数是产量在区间
上的果树株数是产量在区间![]() 上的果树株数的
上的果树株数的![]() 倍。
倍。
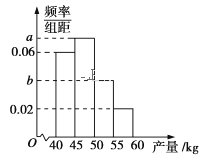
(1)求![]() 的值;
的值;
(2)求样本的平均数和中位数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com